Внутренний узел дерева разбора может быть отмечен

Что такое “внутренний узел” в дереве двоичного поиска?

Теперь вы можете передать параметр любому контроллеру из всего приложения.

6 ответов

 I ROOT (root is also an INTERNAL NODE, unless it is leaf) / \ I I INTERNAL NODES / / \ o o o EXTERNAL NODES (or leaves) 

, Поскольку замечательное изображение показывает, внутренние узлы являются узлами, расположенными между корнем дерева и листами. Обратите внимание, что корень является также внутренним узлом кроме случая, это — единственный узел дерева.

то, Что сказано в одном из сайтов о внутреннем узле, имеющем необходимость иметь двух детей, для дерева, чтобы быть полным двоичным деревом, не для узла, чтобы быть внутренним.

Насколько я понимаю его, это — узел, который не является листом.

внутренний узел или внутренний узел являются любым узлом дерева, которое имеет дочерние узлы и является таким образом не вершиной. Промежуточный узел между корнем и вершинами называют внутренним узлом.

Обычно внутренний узел является любым узлом, который не является листом (узел без детей).

В расширенных двоичных деревьях (также деревья сравнения), внутренние узлы у всех есть два ребенка, потому что каждый внутренний узел соответствует сравнению, которое должно быть сделано [Искусством программирования (TAoCP) vol.3 Сортировкой и Поиском, обсуждением и числом в разделе 5.3.1, p.181 (редактор 2). Между прочим, использование этих деревьев для представления соединений (и byes) для турниров устранения обращено в разделе 5.4.1 из этого материала.]

схема Vinko отражает это различие, хотя корневой узел является также всегда или внутренним узлом или вершиной, в дополнение к тому, чтобы быть единственным узлом без родителя.

существует более широкое обсуждение в обработке Knuth информационных структур и свойствах деревьев [TAoCP vol.1 Фундаментальные Алгоритмы, обсуждение длин пути в деревьях в разделе 2.3.4.5, p.p. 399-406 (редактор 3) включая упражнения (многие работали позади книги)].

полезно заметить, что деревья двоичного поиска (где внутренние узлы также содержат единственные значения, а также наличие до двух детей) несколько отличающиеся [TAoCP vol.3, разделяют 6.2.2]. Номенклатура все еще работает, все же.

Источник

16. Построение дерева синтаксического разбора.

Дерево разбора может рассматриваться как графическое представление порождения, из которого удалена информация о порядке замещения не терминалов.

Каждый внутренний узел дерева представляет применение продукции.

Внутренний узел дерева помечен нетерминалом А из заголовка соответствующей продукции, а дочерние узлы слева направо символами из тела продукции, использованные в порождении для замены А.

Например, дерево для разбора – (id+id):

Листья дерева разбора не терминальными или терминальными и будучи прочитаны слева на право, образуют сентенциальную форму называемую кроной или границей дерева.

Для того что бы увидеть связь между порождениями и деревьями разбора рассмотрим произвольное приведение. α₁ → α₂ → … → α_n

Где альфа 1 отдельный не терминал А.

Для каждой сентенциальной формы альфа 1 можно построить дерево разбора, кроной которого является альфа 1 этот процесс представляет собой индукцию по i.

Пример, последовательность деревьев разбора:

Для моделирования этого шага корню Е в начало дерева добавляют два дочерних узла помеченных «-» и «Е».

2) – E => — (E) добавляют 3 дочерних узла, помеченных (, Е, ) к листу Е для получения дерева с кроной – (Е).

Продолжая построение описываемым способом получается полноценное дерево разбора.

Т.к. дерево разбора игнорирует порядок, в котором производилось замещение символов в сентенциальной форме, между порождениями и деревьями возникает соотношение «многих к одному».

Каждое дерево связано с единственным левым и единственным правым порождением.

17. Нисходящий синтаксический анализ

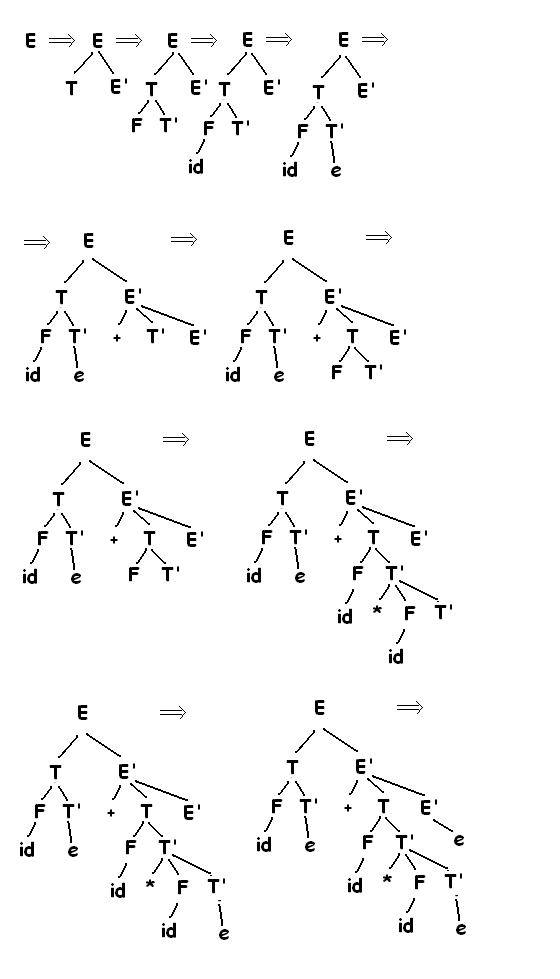
Можно рассмотреть как поиск левого порождения входящей строки. Рассмотрим последовательность построений деревьев разбора для входящей строки (id+id)*id, представляющий собой нисходящий синтаксический анализ, построенный в соответствии с грамматикой:

Эта последовательность деревьев соответствует левому порождению входящей строки. На каждом шаге нисходящего синтаксического анализа ключеваой проблемой является определение продукции, применимой для нетерминалов, например А. Когда А продукция выбрана, остальные части процесса синтаксического анализа состоят из проверки соответвствий терминальных символов в теле продукции входящей строки. В рассмотренном примере строится дерево с двумя узлами, помеченными E’, в первом (в прямом) порядке обхода узла Е’ выбирается продукция

E’ -> +TE’, во втором E’ -> e. Синтаксический анализатор может выбрать нужную E’ продукцию, рассматривающую очередной входящий символ. Класс Грамматик для которых можно построить синтаксический анализатор, просматривающий k-символов во входящем потоке называется классом LL(k).

Метод рекурсивного спуска

Программа синтаксического анализатора методом рекурсивного спуска состоит из набора процедур по одной для каждого нетерминала. Работа программы начинается с вызова процедуры для стартового символа и успешно заканчивается в случае сканирования всей входящей строки.

Типичная процедура для нетерминала низходящего анализатора

If (Xi-нетерминал) Вызов процедуры Xi();

else if(Xi равно текущему входному символу a)

Переход к следующему входному символу

Этот псевдокод недетерминирован т.к. он начинается с выбором А-продукции не указанным способом.

Рекурсивный способ в общем случае может потребовать выполнения возврата т.е. повторения сканирования входного потока. При анализе синтаксической конструкции языка программирования возврат требуется редко. В ситуациях , наподобие, синтаксического анализа естественного языка возврат не слишком эффективен и предпочтительней являются табличные методы. Чтобы разрешить возврат код в примере должен быть модифицирован:

1. Невозможно выбрать единую А-продукцию в строке (1), поэтому требуется испытывать каждую из нескольких продукций в некотором порядке.
2. Ошибка в строке (*) не является окончательной и предполагает возворат к строке (1) и испытание другой А-продукции.

Объявлять о найденной во входной строке ошибке можно только в том случае, если больше не имеется непроверенных А-продукций.

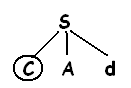
Чтобы построить дерево разбора для входной строки ω-cod начинают с дерева, состоящего из единичного узла с меткой S и указателя входного потока, указывающего на С или первый символ ω.

S имеет единичную продукцию, поэтому ее используют для разворачивания и получения дерева.

Соответствует первому символу входного потока ω, поэтому указатель входного потока перемещается к а-второму символу ω и рассматривается следующий лист, помеченный А.

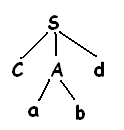
Затем разворачивается А с использованием альтернативы А -> ab и получаем таким образом дерево, показанное на рис.

Имеется совпадение второго входного символа а, поэтому выполняется переход к третьему символу d и сравнивают его с очередным листком b. Т.к. b не соответствует d, то сообщается об ошибке и происходит возврат к А.

Чтобы выяснить нет ли альтернативной продукции, которая не была проверена до этого времени, вернувшись к а необходимо отбросить указатель входного потока так, чтобы он указывал на позицию 2, в которой указатель находится, когда впервые столкнулся с а. Это означает что процедура для а должна хранить указатель на входной поток в локальной переменной.

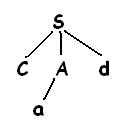
Вторая альтернатива для а дает дерево разбора:

Лист а соответствует второму символу ω, а лист d – третьему символу. Т.к. построено дерево разбора для входящей строки ω, то алгоритм завершает работу и сообщает об успешном выполнении синтаксического анализа и построении дерева разбора. Левосторонняя грамматика может привести синтаксический анализатор, работающий методом рекурсивного спуска к бесконечному циклу, т.е. когда пытаются проверить нетерминал а, то в конечном счете можно найти этот же нетерминал а и перейти к попытке развернуть а, так и не взяв ни одного символа из входного потока.

Источник

41.Деревья разбора. Определения. Свойства. Примеры.

Дерево разбора – это дерево, показывающее сущность порождения. Внутрение узлы отмечены переменными, листья – терминалами или ε. Для каждого внутренего узла должна существовать продукция , голова которой является отметкой узла, а отметки сыновей узла, прочитанные слева направо, образуют её тело.

Терминальная цепочка принадлежит языку граматики т. И т.т, когда она является кроной, по крайней мере одного дерева разбора. таким образом существование левых и правых порождений и деревьев разбора является равносильным условием того, что все они определяют в точности цепочки языка КС- граматики. Для некоторых граматик можно найти терминальную цепочку с несколькими деревьями разбора, или (что равносильно) с несколькими левыми или правыми порождениями. Такая граматика называется неоднозначной.

Любой узел дерева отмечен переменными из множества …. 2) любой лист дерева отмечен… либо терминалом, либо пустым символом

Особый интерес представляют деревья со следущими св-ми

42.Связь ксг с конечными автоматами. Нормальная форма Хомского.

По любой заданой КСГ можно наблюдать одну КСГ которая порождает тот же язык что и исходная за искл. Цепочки эпсилон, и при этом новая граматика находиться в нормальной форме Хомского т.е не содержит бесполезных символов и тела каждой продукчии состоит либо из 2–х переменных либо из одного терминала

переменнные можно удалить из граматики если она не порождает не одной терминальной цепочки, или не встречает в чепочках выводимых из стартового символа

2) удаляются цепные и и эпсилон продукции

43. Принцип микропрограммного управления. Теорема Глушкова. Понятия операционного и управляющих автоматов.

Функциональная и структурная организация выч. Устройств

1. любая операция релизуемая устройством, которая расссматривает как элементарные действия операций. Передача информации из одного устройства в другое
2. для управления используются логические условия зависисмости от результата, могут принимать значения либо истины (1) либо лжи(0)
3. процес выполнения операций в устройстве описывается в форме алгоритма который представляется в терминах микроопераций и логических условий и называется микропрограммой. Она определяет порядок следования операций и необходима для получения результата
4. используется как форма представления функций устройства на основе которой определяется порядок функционирования устройства во врепени

академиком глушковым было показано что в любом устройстве обработки информации, операционный автомат это:

выпонение логических условий

Значение логических условий в операционном автомате задаются множеством осведомительных сигналов.

Управляющий автомат генерирует последовательность управляющих сигналов предписаную микропрограммой и соответственым значение логических условий

Операционый автомат задается 5 множествами

1. мн-во вх слов Д
2. мн-во выходных слов R
3. мн-во внутрених слов S
4. мн-во микроопераций У (преобразование вхю слов в выходные)
5. лог. Условие х

Источник