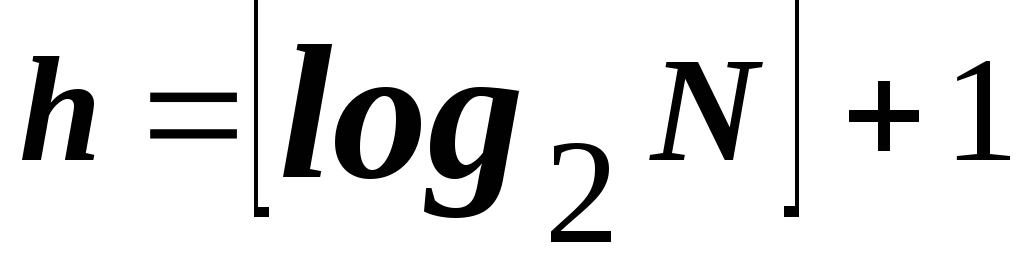Все виды бинарных деревьев

Двоичное дерево

Двоичное дерево — древовидная структура данных, в которой у родительских узлов не может быть больше двух детей.

Типы двоичных деревьев

Полное двоичное дерево

Полное двоичное дерево — особый тип бинарных деревьев, в котором у каждого узла либо 0 потомков, либо 2.

Совершенное двоичное дерево

Совершенное двоичное дерево — особый тип бинарного дерева, в котором у каждого внутреннего узла по два ребенка, а листовые вершины находятся на одном уровне.

Законченное двоичное дерево

Законченное двоичное дерево похоже на совершенное, но есть три большие отличия.

1. Все уровни должны быть заполнены.
2. Все листовые вершины склоняются влево.
3. У последней листовой вершины может не быть правого собрата. Это значит, что завершенное дерево необязательно полное.

Вырожденное двоичное дерево

Вырожденное двоичное дерево — дерево, в котором на каждый уровень приходится по одной вершине.

Скошенное вырожденное дерево

Скошенное вырожденное дерево — вырожденное дерево, в котором есть либо только левые, либо только правые узлы. Таким образом, есть два типа скошенных деревьев — скошенные влево вырожденные деревья и скошенные вправо вырожденные деревья.

Сбалансированное двоичное дерево

Сбалансированное двоичное дерево — тип бинарного дерева, в котором у каждой вершины количество вершин в левом и правом поддереве различаются либо на 0, либо на 1.

Представление двоичного дерева

Узел двоичного дерева можно представить структурой, содержащей данные и два указателя на другие структуры того же типа.

Примеры реализации

Python

# Двоичное дерево в Python class Node: def __init__(self, key): self.left = None self.right = None self.val = key # Прямой обход дерева def traversePreOrder(self): print(self.val, end=' ') if self.left: self.left.traversePreOrder() if self.right: self.right.traversePreOrder() # Центрированный обход дерева def traverseInOrder(self): if self.left: self.left.traverseInOrder() print(self.val, end=' ') if self.right: self.right.traverseInOrder() # Обратный обход дерева def traversePostOrder(self): if self.left: self.left.traversePostOrder() if self.right: self.right.traversePostOrder() print(self.val, end=' ') root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) print("Прямой обход дерева: ", end="") root.traversePreOrder() print("\nЦентрированный обход дерева: ", end="") root.traverseInOrder() print("\nОбратный обход дерева: ", end="") root.traversePostOrder()

Java

// Двоичное дерево на Java // Создание узла class Node < int key; Node left, right; public Node(int item) < key = item; left = right = null; >> class BinaryTree < Node root; BinaryTree(int key) < root = new Node(key); >BinaryTree() < root = null; >// Центрированный обход дерева public void traverseInOrder(Node node) < if (node != null) < traverseInOrder(node.left); System.out.print(" " + node.key); traverseInOrder(node.right); >> // Обратный обход дерева public void traversePostOrder(Node node) < if (node != null) < traversePostOrder(node.left); traversePostOrder(node.right); System.out.print(" " + node.key); >> // Прямой обход дерева public void traversePreOrder(Node node) < if (node != null) < System.out.print(" " + node.key); traversePreOrder(node.left); traversePreOrder(node.right); >> public static void main(String[] args) < BinaryTree tree = new BinaryTree(); tree.root = new Node(1); tree.root.left = new Node(2); tree.root.right = new Node(3); tree.root.left.left = new Node(4); System.out.print("Прямой обход дерева: "); tree.traversePreOrder(tree.root); System.out.print("\nЦентрированный обход дерева: "); tree.traverseInOrder(tree.root); System.out.print("\nОбратный обход дерева: "); tree.traversePostOrder(tree.root); >>

Си

// Обход дерева на Си #include #include struct node < int item; struct node* left; struct node* right; >; // Центрированный обход дерева void inorderTraversal(struct node* root) < if (root == NULL) return; inorderTraversal(root->left); printf("%d ->", root->item); inorderTraversal(root->right); > // Прямой обход дерева void preorderTraversal(struct node* root) < if (root == NULL) return; printf("%d ->", root->item); preorderTraversal(root->left); preorderTraversal(root->right); > // Обратный обход дерева void postorderTraversal(struct node* root) < if (root == NULL) return; postorderTraversal(root->left); postorderTraversal(root->right); printf("%d ->", root->item); > // Создание нового узла struct node* createNode(value) < struct node* newNode = malloc(sizeof(struct node)); newNode->item = value; newNode->left = NULL; newNode->right = NULL; return newNode; > // Вставка потомка слева от родительской вершины struct node* insertLeft(struct node* root, int value) < root->left = createNode(value); return root->left; > // Вставка потомка справа от родительской вершины struct node* insertRight(struct node* root, int value) < root->right = createNode(value); return root->right; > int main() < struct node* root = createNode(1); insertLeft(root, 2); insertRight(root, 3); insertLeft(root->left, 4); printf("Центрированный обход дерева\n"); inorderTraversal(root); printf("\nПрямой обход дерева\n"); preorderTraversal(root); printf("\nОбратный обход дерева\n"); postorderTraversal(root); >

С++

// Двоичное дерево на С++ #include #include using namespace std; struct node < int data; struct node *left; struct node *right; >; // Создание нового узла struct node *newNode(int data) < struct node *node = (struct node *)malloc(sizeof(struct node)); node->data = data; node->left = NULL; node->right = NULL; return (node); > // Прямой обход дерева void traversePreOrder(struct node *temp) < if (temp != NULL) < cout data; traversePreOrder(temp->left); traversePreOrder(temp->right); > > // Центрированный обход дерева void traverseInOrder(struct node *temp) < if (temp != NULL) < traverseInOrder(temp->left); cout data; traverseInOrder(temp->right); > > // Обратный обход дерева void traversePostOrder(struct node *temp) < if (temp != NULL) < traversePostOrder(temp->left); traversePostOrder(temp->right); cout data; > > int main() < struct node *root = newNode(1); root->left = newNode(2); root->right = newNode(3); root->left->left = newNode(4); cout

Где используется

• Для быстрого доступа к данным.
• В алгоритмах маршрутизации.
• Для реализации куч.
• В синтаксических деревьях.

Источник

7.5. Виды бинарных деревьев

Дерево называется идеально сбалансированным, если число узлов в его правом и левом поддеревьях отличается не более чем на единицу(далее будем называть такие деревья сбалансированными). Сбалансированное дерево, состоящее изNузлов, имеет минимальную высоту среди всех бинарных деревьев. Высоту сбалансированного дерева можно определить по формуле:

.

Минимальная высота при заданном числе узлов достигается, если на всех уровнях, кроме последнего, размещается максимально возможное число узлов. Это происходит за счет равномерного размещения узлов поровну слева и справа от каждого узла.

Правило равномерного размещения для Nузлов (правило 1) формулируется с помощью рекурсии:

• взять один узел в качестве корня;
• по правилу 1построить левое поддерево с числом узловnl = N div 2;
• по правилу 1построить правое поддерево с числом узловnr=N— nl — 1.

Структура сбалансированного дерева из Nузлов определяется количеством узлов (рис. 69). N = 5Рис. 69. Сбалансированное дерево Процедура построения сбалансированного дерева из Nузлов:

Type

PTree = ^ Tree;

Tree = record

info: char;

left, right: PTree

end;

Procedure Balance( var root: PTree;

n: byte );

begin

if n = 0 then root:=nil

else begin

new( root );

write( ‘Значение инф. поля‘, i, ‘-го узла дерева = ‘ );

readln( root^.info );

Balance( root^.left, n div 2);

(*1*) Balance( root^.right, n – n div 2 – 1)

(*2*) end

(*3*)end;

Таблица 5. Трасса состояний стека при работе процедуры построения сбалансированного дерева

Номер уровня рекур- сии	Знач-я входного парам-раn	Стек		Знач-я вых. пар-ра			Выход
		Исходное состояние(n,root, (.)возврата)	Конечное состояние(n,root, (.)возврата)	root	root^.left	root^.right	из уровня
1	3	(-, -, -)	(3,^A, *1*)	^A	—	—	—
2	1	(3,^A, *1*)	(1, ^B, *1*) (3, ^A, *1*)	^B	—	—	—
3	0	(1, ^B, *1*) (3, ^A, *1*)	(0,NIL,*1*) (1, ^B, *1*) (3, ^A, *1*)	NIL	—	—	—
	0	(0,NIL,*1*) (1, ^B, *1*) (3, ^A, *1*)	(1, ^B, *1*) (3, ^A, *1*)	NIL	—	—	(* 3 *)
2	1	(1, ^B, *1*) (3, ^A, *1*)	(1, ^B, *2*) (3, ^A, *1*)	^B	NIL	—	—
3	0	(1, ^B, *2*) (3, ^A, *1*)	(0,NIL,*2*) (1, ^B, *2*) (3, ^A, *1*)	NIL	—	—	—
	0	(0,NIL,*2*) (1, ^B, *2*) (3, ^A, *1*)	(1, ^B, *2*) (3, ^A, *1*)	NIL	—	—	(* 3 *)
2	1	(1, ^B, *2*) (3, ^A, *1*)	(3, ^A, *1*)	^B	NIL	NIL	(* 3 *)
1	3	(3, ^A, *1*)	(3, ^A, *2*)	^A	^B	—	—
2	1	(3,^A, *2*)	(1, ^С, *1*) (3, ^A, *2*)	^C	—	—	—
3	0	(1, ^С, *1*) (3, ^A, *2*)	(0,NIL,*1*) (1, ^С, *1*) (3, ^A, *2*)	NIL	—	—	—
	0	(0,NIL,*1*) (1, ^С, *1*) (3, ^A, *2*)	(1, ^С, *1*) (3, ^A, *2*)	NIL	—	—	(* 3 *)
2	1	(1, ^С, *1*) (3, ^A, *2*)	(1, ^С, *2*) (3, ^A, *2*)	^C	NIL
3	0	(1, ^С, *2*) (3, ^A, *2*)	(0,NIL,*2*) (1, ^С, *2*) (3, ^A, *2*)	NIL	—	—	—
	0	(0,NIL,*2*) (1, ^С, *2*) (3, ^A, *2*)	(1, ^С, *2*) (3, ^A, *2*)	NIL	—	—	(* 3 *)
2	1	(1, ^С, *2*) (3, ^A, *2*)	(3, ^A, *2*)	^C	NIL	NIL	(* 3 *)
1	3	(3, ^A, *2*)	(-, -, -)	^A	^B	^C	(* 3 *)

Для иллюстрации работы этой процедуры и построения трассы состояний стека будем использовать следующие обозначения: ^A– адрес узла дерева, в информационном поле которого хранится символ“A”; (* 1 *) и (* 2 *) – адреса возврата из уровня рекурсивной процедуры, номер которой на 1 больше текущего; (* 3 *) – адрес возврата из рекурсивной процедуры текущего уровня. Трасса построения сбалансированного дерева, содержащего 3 узла, приведена в таблице 5. Сбалансированное дерево, как и дерево любого другого вида, можно построить в процессе нисходящего обхода. Особенность работы процедуры построения дерева заключается в том, что сначала создаются корневые узлы, адреса которых запоминаются в стеке. Установить ссылки из корневых узлов дерева на их поддеревья можно только после того, как эти поддеревья будут созданы и адреса их корневых узлов возвращены в точки вызова. Точками вызова являются поля ссылок на левое поддерево (root^.left) или правое поддерево(root^.right) корневого узла (в таблице установка этих ссылочных связей показана стрелками). Подобная возможность обеспечивается за счет того, чтоуказатель на корень дерева является параметром-переменной процедуры.

Источник