Вычисление глубины бинарного дерева

Как рассчитать глубину бинарного дерева поиска

Я хотел бы рассчитать суммирование глубин каждого node двоичного дерева поиска. Индивидуальные глубины элементов еще не сохранены.

Изменение вопроса после того, как люди предоставили ответы, заставит первоначальные ответы казаться не связанными с последним вопросом. Также вы не можете принять два ответа. Было бы лучше задать новый вопрос, т.е. на новой странице. Вы также можете принять ответ на оригинальный вопрос.

10 ответов

int countChildren(Node node)

И чтобы получить сумму глубин каждого ребенка:

int sumDepthOfAllChildren(Node node, int depth) < if ( node == null ) return 0; // starting to see a pattern? return depth + sumDepthOfAllChildren(node.getLeft(), depth + 1) + sumDepthOfAllChildren(node.getRight(), depth + 1); >

Теперь, надеюсь, информативное объяснение в случае, если это домашнее задание. Подсчет количества узлов довольно прост. Прежде всего, если node не является node ( node == null ), он возвращает 0. Если это node, он сначала подсчитывает свое «я» ( 1 ), а также число узлов в его левом поддереве плюс число узлов в его правом поддереве. Еще один способ подумать — вы посещаете каждый node через BFS и добавляете его к счету для каждого node, который вы посещаете.

Суммирование глубин аналогично, за исключением того, что вместо добавления только одного для каждого node, node добавляет глубину его самого. И он знает глубину своего «я», потому что его родитель рассказал об этом. Каждый node знает, что глубина его детей — это собственная глубина плюс одна, поэтому, когда вы получаете глубину левого и правого дочерних элементов node, вы сообщаете им, что их глубина — это текущая глубина node плюс 1.

И снова, если node не является node, он не имеет глубины. Поэтому, если вам нужна сумма глубины всех корневых node детей, вы передаете в корневой каталог node и корневую глубину node следующим образом: sumDepthOfAllChildren(root, 0)

Рекурсия весьма полезна, это совсем другой способ думать о вещах и берет практику, чтобы привыкнуть к ней

Источник

Основная идея реализации бинарного дерева с Golang

Для общих операций алгоритма есть не что иное, как три основные операции записи, поиска и удаления. Кроме того, могут быть некоторые операции, такие как получение информации о соответствующей структуре данных. Например, бинарному дереву может потребоваться получить степень дерева, а стекам и очередям — длину.

Согласно этой идее, нам нужно понять это для работы с бинарным деревом:

1. Определение структуры бинарного дерева
2. Создание бинарного дерева
3. Добавление данных в бинарное дерево
4. Подсчитать количество узлов в бинарном дереве
5. Вычислить глубину бинарного дерева
6. Обход бинарного дерева: четыре метода обхода

1. Обход в предварительном порядке: сначала посетите корневой узел, затем посетите левое поддерево и, наконец, посетите правое поддерево; это повторяется до конца.
2. Обход в обратном порядке: сначала посетите левое поддерево, затем посетите правое поддерево и, наконец, посетите корневой узел; это повторяется до конца.
3. Обход по порядку: сначала посетите левое поддерево, затем посетите корневой узел и, наконец, посетите правое поддерево; это повторяется до конца.
4. Иерархический обход: каждый уровень посещает каждый узел слева направо.

Структура бинарного дерева.

Проектирование структуры бинарного дерева. Используйте характеристики односторонней связанной таблицы и сходство с двоичным деревом для проектирования.

1. Дерево представляет собой рекурсивную форму, оно связано и хранится между каждым узлом.
2. Бинарное дерево имеет только левое и правое поддеревья

Создание бинарного дерева.

Основная идея состоит в том, чтобы создать бинарное дерево, используя характеристики односторонней цепной таблицы (собственно, здесь ее нельзя назвать односторонней цепной таблицей, потому что это должна быть односторонняя цепная таблица; корневой узел указывает на два дочерних узла), поэтому узлы бинарного дерева являются узлами цепной таблицы.

func CreateNode(v int) *TreeNode < return &TreeNode> 

Добавление данных в бинарное дерево.

Основная идея состоит в том, чтобы начать только с одного корневого узла, затем по мере необходимости либо в направлении левого поддерева, либо в направлении правого поддерева, и просто связать напрямую с новым узлом, и так далее и тому подобное.

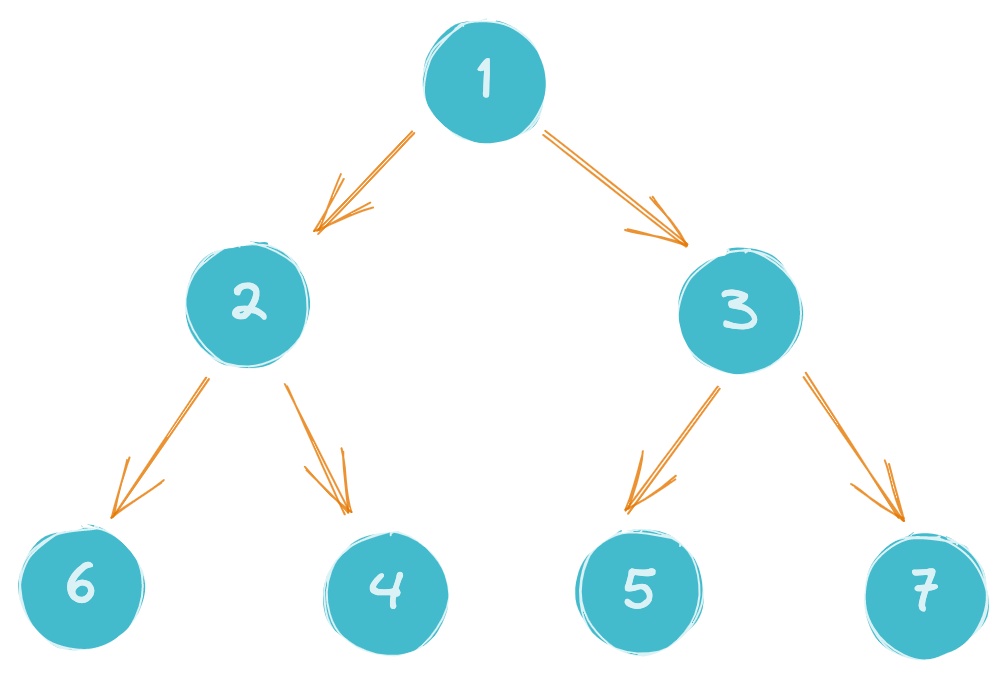
Схематическая диаграмма результата выглядит следующим образом:

Подсчет количества узлов в бинарном дереве.

Мы используем приведенный выше пример для тестирования. Поскольку бинарное дерево является рекурсивной структурой, мы можем использовать рекурсию для обхода вычислений.

func (root *TreeNode) GetTreeNodeNum() int < if root == nil < return 0 >else < // calculate the number of nodes under the left node // calculate the number of nodes under the right node // and finally add the number of root nodes. return root.Left.GetTreeNodeNum() + root.Right.GetTreeNodeNum() + 1 >> 

Вычисление глубины бинарного дерева.

Глубина дерева также является максимальным уровнем дерева.

Корневой узел — это первый уровень, и пока существует левое поддерево или существует правое поддерево, уровень нужно добавить на единицу, и расчет продолжается до конца.

Таким образом, это можно сделать снова с помощью рекурсии.

func (root *TreeNode) GetTreeDegree() int < maxDegree := 0 if root == nil < return maxDegree >if root.Left.GetTreeDegree() > root.Right.GetTreeDegree() < maxDegree = root.Left.GetTreeDegree() >else < maxDegree = root.Right.GetTreeDegree() >return maxDegree + 1 > 

Обход четырех видов бинарных деревьев.

Первые три являются простыми, используя рекурсивные методы, а четвертый метод более сложен.

Для обхода бинарного дерева в прямом порядке выполняются следующие операции:

1. Посетите корень.
2. Обходим левое поддерево корня.
3. Пройдите по правому поддереву корня.

func (root *TreeNode) PreOrder() < if root != nil < // print root fmt.Print(root.Data, " ") // print left tree root.Left.PreOrder() // print right tree root.Right.PreOrder() >> 

Для приведенного выше примера результат должен быть выведен 1 2 6 4 3 5 7 .

Для обхода бинарного дерева в обратном порядке выполняются следующие операции:

1. Обходим левое поддерево корня.
2. Пройдите по правому поддереву корня.
3. Посетите корень.

func (root *TreeNode) PostOrder() < if root != nil < // print left tree root.Left.PostOrder() // print right tree root.Right.PostOrder() // print root fmt.Print(root.Data, " ") >> 

Для приведенного выше примера результат должен быть выведен 6 4 2 5 7 3 1 .

Для обхода бинарного дерева в порядке обхода выполняются следующие операции:

1. Пройдите по самому левому поддереву.
2. Посетите корень.
3. Пройдите по самому правому поддереву.

func (root *TreeNode) MidOrder() < if root != nil < // print left tree root.Left.MidOrder() // print root fmt.Print(root.Data, " ") // print right tree root.Right.MidOrder() >> 

Для приведенного выше примера результат должен быть выведен 6 2 4 1 5 3 7 .

Поскольку это древовидная структура и требуется выводить результаты слой за слоем, после вывода значения левого узла необходимо вывести значение правого узла этого слоя.

Предыдущие три метода соответствуют способу вывода модели «небольшое трехузловое дерево», поэтому эти три метода не могут сразу найти нужный узел по соседству.

Таким образом, мы можем рассмотреть возможность создания кэша очереди (функция «первым поступил — первым обслужен»), обхода данных и помещения их в очередь в порядке вывода.

Таким образом, решение состоит в том, чтобы реализовать каждый уровень для доступа к каждому узлу слева направо.

Во-первых, поместите корневой узел дерева в очередь, вам нужно определить очередь таблицы цепочки.

Удалите узел из очереди, сначала выведите значение узла, если узел имеет левый узел поддерева, левое поддерево отправляется в стек, если узел имеет правый узел поддерева, правое поддерево отправляется в стек.

Повторяйте до тех пор, пока в очереди не останется элементов.

func (root *TreeNode) LayerOrder() < if root == nil < return >// new a queue queue := new(LinkQueue) // add root queue.Add(root) for queue.size > 0 < // Constantly out of queue element := queue.Remove() fmt.Print(element.Data, " ") // The left subtree is not empty and is in the queue if element.Left != nil < queue.Add(element.Left) >// The right subtree is not empty and is in the queue if element.Right != nil < queue.Add(element.Right) >> > 

Полный код обхода бинарного дерева по уровням.

type LinkNode struct < Next *LinkNode Value *TreeNode >// Chained queue, first in first out type LinkQueue struct < root *LinkNode // Starting point of the chain table size int // Number of elements in the queue lock sync.Mutex // Locks used for concurrent security >// in func (queue *LinkQueue) Add(v *TreeNode) < queue.lock.Lock() defer queue.lock.Unlock() // If the top of the stack is empty, then add the node if queue.root == nil < queue.root = new(LinkNode) queue.root.Value = v >else < // Otherwise the new element is inserted at the end of the chain newNode := new(LinkNode) newNode.Value = v // Traverse all the way to the end of the chain nowNode := queue.root for nowNode.Next != nil < nowNode = nowNode.Next >// The new node is placed at the end of the chain nowNode.Next = newNode > // Number of elements in the queue +1 queue.size = queue.size + 1 > // func (queue *LinkQueue) Remove() *TreeNode < queue.lock.Lock() defer queue.lock.Unlock() // empty queue if queue.size == 0 < panic("over limit") >// pop the top element topNode := queue.root v := topNode.Value // Chain the top element's successor links queue.root = topNode.Next // Number of elements in the queue -1 queue.size = queue.size - 1 return v > 

Источник

how to find the height of a node in binary tree recursively

this is my sample code for find the Height, is defined as the length of the longest path by number of nodes from self to a leaf. The height of a leaf node is 1. it doesn’t work.

Actually, I just need an algorithm. Because, my code doesn’t work. And if you know the solution, maybe pseudo code 😛

@thg435 My guess is: «why doesn’t it work?» The poster seems to be struggling with English, so I would give him a break here. That being said, I wouldn’t give the code (since it looks like a homework to me), but explain some of the more blatant mistakes that he made.

@TGulmammadov: two options. Option 1: draw a tree on a piece of paper and try to find the height for any given node manually. Note your steps. Try to describe what you’re doing first in pseudocode and then in python. Option 2: sit back and wait for some nice guy to post the codez for you.

Do you have an example where it fails? How does it fail? Let me guess: it always counts the depth of the leftmost path, not of arbitrary paths?

6 Answers 6

What you’re doing isn’t recursive, it’s iterative. Recursive would be something like:

def height(node): if node is None: return 0 else: return max(height(node.left), height(node.right)) + 1 

return max(height(node.left), height(node.right)) + 1 returns a value >= 1 however leaf nodes have height zero. @mata Could you please clarify. Thanks.

@harishvc — Looking at the edit history, I had return -1 , which means a leaf would have a height of 0 (which is usually how the hight of a tree is defined), but the OP specified «The height of a leaf node is 1», so that’s probably why I changed it.

A leaf node will have None for node.left and node.right , therefore ending the recursion there, there’s no need to treat leaf or inner or root nodes differently.

@Illusionist — for any node the height ist the height of it’s largest child tree (that’s what the max function does) + 1. For a leaf node where both node.left and node.right are None heigh will return 0 for both and the recursion ends there.

You were given the solution by mata, but I suggest you also look at your code and understand what it is doing:

 while self.right != None: self = self.right path = path +1 

What will this do? it will find the right child, then its right child, and so on. So this checks only one path of the «rightmost» leaf.

This does the same for the left:

 while self.left != None: self = self.left path = path +1 

The idea in recursion is that for each subproblem, you solve it using the exact same recipe for all other subproblems. So if you would apply your algorithm only to a subtree or a leaf, it would still work.

Also, a recursive definition calls itself (although you can implement this with a loop, but that is beyond the scope here).

Recursion: see definition of Recursion.

Источник