Тема 3.7 Деревья
Определение: Деревом называется связный, ориентированный граф без петель и кратных ребер, не содержащий в себе циклов, удовлетворяющий следующим условиям:
- имеется в точности один узел, называемый корнем, в который не входит ни одно ребро,
- В каждый узел, кроме корня, входит ровно одно ребро,
- Из корня к каждому узлу идет путь ( который, как легко показать единственный).
Деревья являются простейшим видом связных графов. Любое дерево с n вершинами содержит n-1 ребер. Число различных деревьев, которые можно построить на n вершинах равно 
Определение Дерево с одной выделенной вершиной называется корневым деревом. Определение Ориентированный граф, состоящий из нескольких деревьев, называется лесом. Определение: Пусть G=(Х, Г) – граф, являющийся лесом. Если дуга (v,w) принадлежит Г, то v называется отцом узла w, а w – сыном узла v. Определение: Если есть путь из v в w, то v называется предком узла w, а w – потомком узла v. Определение: Узел без потомков называется листом. Определение: Узел v и его потомки вместе образуют поддерево леса G, и узел v называется корнем этого поддерева. Определение:Глубина узла v в дереве – это длина пути из корня в v. Определение:Высота узла в дереве – это длина самого длинного пути из этого узла в какой-нибудь лист. Определение:Высотой дерева называется высота его корня. Пример 
Глубина узла b, в данном примере, = 1, а его высота = 2. Высота дерева = 3. Определение:Упорядоченным деревом называется дерево, в котором множество сыновей каждого узла упорядоченно. При изображении упорядоченного дерева, как правило, считается, что множество сыновей каждого узла упорядоченно слева направо. Определение:Бинарным деревом называется такое упорядоченное дерево, что
- Каждый сын произвольного узла идентифицируется либо как левый сын, либо как правый сын.
- Каждый узел имеет не более одного левого и не более одного правого сына.
Обратите внимание, что бинарное дерево не является частным случаем дерева, это совершенно иное, хотя и тесно связанное понятие. Н
апример: Указанные бинарные деревья различны между собой ( в первом случае корень имеет пустое правое поддерево, а во втором левое поддерево пусто), хотя как деревья они изоморфны, и мы можем рассматривать их как одно дерево. Определение: Бинарное дерево называется полным, если для некоторого целого числа K каждый узел, глубины меньшей k имеет как левого, так и правого сына, и каждый узел глубины k является листом. Полное дерево глубины k имеет 
узлов. Очень часто используются алгоритмы, которые проходят дерево (посещают каждый его узел) в некотором порядке. Известно несколько способов сделать это. Мы рассмотрим три широко известных способа: прохождение дерева в прямом порядке, обратном порядке и внутреннем. Будем считать, что Т – дерево с корнем r и сыновьями при k >=0. При k = 0 это дерево состоит из единственного узла r.
Прохождение дерева т в прямом порядке определяется следующим алгоритмом:
- Посетить корень r
- Посетить слева на право поддеревья с корнями v1 . . . vk в указанной последовательности.
П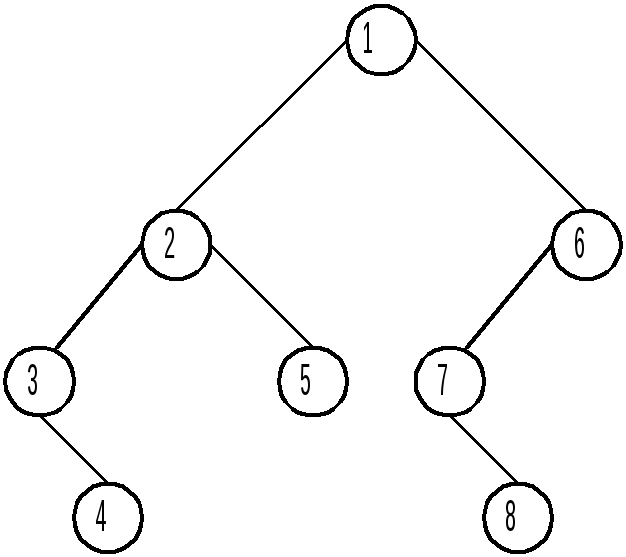
ример Прохождение дерева Т в обратном порядке определяется следующим алгоритмом: Посетить в обратном порядке поддеревья с корнями v1 . . . vk в указанной последовательности. Посетить корень r П
ример Прохождение дерева Т во внутреннем порядке определяется следующим алгоритмом: Посетить во внутреннем порядке левое поддерево корня (если оно существует). Посетить корень Посетить во внутреннем порядке правое поддерево корня (если оно существует). Пример П
режде чем дать описание одного из этих алгоритмов на некотором формальном языке программирования, поговорим о способах задания и хранения деревьев и бинарных деревьев. Очень многие объекты представимы в виде деревьев. Например: сложная нумерация глав лекций – типичный информационный объект, сохраняемый и обрабатываемый в виде дерева. 1. Теория графов 1.1. Основные определения теории графа 1.2. Операции над графами 1.2.1. Одноместные операции 1.2.2. Двуместные операции 1.3. Отношения 1.3.1. Отношение порядка 1.3.2. Отношение эквивалентности
- Числовые характеристики графа
1.5. Понятие обхода графа 1.5.1. Эйлеров цикл 1.5.2. Гамильтонов цикл
- Изоморфизм графов
- Понятие дерева
- Бинарные деревья
- Алгоритмы нумерации узлов графа
- Нумерация в прямом порядке
- Нумерация в обратном порядке
- Нумерация во внутреннем порядке
Подобная система нумерации часто называется десятичной системой обозначения Дьюи. В
ведем интуитивное понятие линейного списка. Мы еще не раз будем говорить об этом способе представления и хранения информации. Одним из распространенных способов хранения деревьев является массив списков. Это одномерный массив, размерностиn – количество узлов дерева. Каждый элемент этого массива – это упорядоченный или неупорядоченный список сыновей этого отца. Например Бинарные деревья, как правило, хранятся посредством двух массивов ЛЕВЫЙСЫН и ПРАВЫЙСЫН, где номер элемента массива – это номер узла, а значение этого элемента – номер левого или правого узла – сына. Если элемент — сын отсутствует, то значение равно 0. Пример Теперь опишем алгоритм нумерации узлов двоичного дерева в соответствии с внутренним порядком. Для этого будем пользоваться неким подобием языка программирования, специально предназначенного для прозрачного и понятного описания алгоритмов. Вход: Двоичное дерево, представленное массивами ЛЕВЫЙСЫН и ПРАВЫЙСЫН. Выход: Массив, называемый НОМЕР, такой, что НОМЕР[i] – номер i – того узла во внутреннем порядке. Метод: Будем использовать глобальную переменную СЧЕТ, значение которой – номер очередного узла в соответствии с внутренним порядком. Начальное значение переменной СЧЕТ = 1. Программа выглядит так: begin СЧЕТ 1 ВНУТРПОРЯДОК(КОРЕНЬ) EndProcedure ВНУТРПОРЯДОК(УЗЕЛ) Begin 1. if ЛЕВЫЙСЫН[УЗЕЛ]0 then ВНУТРПОРЯДОК(ЛЕВЫЙСЫН[УЗЕЛ]); 2. НОМЕР[УЗЕЛ] СЧЕТ;
- СЧЕТ СЧЕТ+1
4. if ПРАВЫЙСЫН[УЗЕЛ]0 then ВНУТРПОРЯДОК(ПРАВЫЙСЫН[УЗЕЛ]); End Такая процедура, которая явно или неявно вызывает сама себя, называется рекурсивной. Применение рекурсии часто дает возможность давать более прозрачное и сжатое описание алгоритма, чем это же можно было бы сделать, не используя рекурсию. Если бы приведенный алгоритм не был записан рекурсивно, надо было бы строить явный механизм для прохождения дерева. Двигаться вниз по дереву нетрудно, но чтобы обеспечить возможность вернуться к предку, надо запомнить всех предков в стеке, а операторы работы со стеком усложнили бы алгоритм, лишив его наглядности.
Источник
Высота и глубина бинарного дерева
Эта статья направлена на то, чтобы провести различие между двумя свойствами бинарных деревьев, называемыми высотой и глубиной. В соответствии с терминологией бинарного дерева ниже приведены определения высоты и глубины бинарного дерева.
Высота. Высота бинарного дерева — это количество ребер на самом длинном пути от корневого узла до самого дальнего конечного узла.
Глубина. Глубина бинарного дерева — это количество узлов на самом длинном пути от корневого узла до самого дальнего конечного узла.
Несколько терминов бинарного дерева
Пустое дерево имеет высоту -1
Дерево только с одним узлом (корневым узлом) имеет высоту 0.
Давайте рассмотрим несколько примеров бинарного дерева, чтобы прояснить разницу.
Давайте посчитаем высоту Дерева 1, Дерева 2, Дерева 3 и Дерева 4
Дерево 1: мы отслеживаем узлы 50–70–60–55, что дает 3 ребра между узлами, следовательно, высота равна 3
Дерево 2: мы отслеживаем узлы 15–20–25, что дает 2 ребра между узлами, следовательно, высота равна 2
Дерево 3: мы отслеживаем узлы 14–15–18–21–25–45, что дает 5 ребер между узлами, следовательно, высота равна 5
Дерево 4: мы отслеживаем узлы 12–14–18–16, что дает 3 ребра между узлами, следовательно, высота равна 3
Давайте посчитаем глубину дерева 1, дерева 2, дерева 3 и дерева 4
Дерево 1: мы считаем узлы 50–70–60–55, что дает 4 узла, следовательно, глубина равна 4.
Дерево 2: мы отслеживаем узлы 15–20–25, что дает 3 узла, следовательно, глубина равна 3
Дерево 3: мы отслеживаем узлы 14–15–18–21–25–45, что дает 6 узлов, следовательно, глубина равна 6
Дерево 4: мы отслеживаем узлы 12–14–18–16, что дает 4 узла, следовательно, глубина равна 4
Давайте посмотрим на приведенный ниже фрагмент кода для определения высоты и глубины двоичного дерева.
Предположим, мы построили деревья от 1 до 4.
public class HeightDepthBST < Node root; int height (Node node) < if (node == null) return 0; else if (node.left == null && node.right == null) return 0; return 1 + Math.max (height(node.left), height(node.right)); > int depth (Node node) < if (node == null) return 0; int left = depth (node.left); int right = depth (node.right); return (left > right) ? left+1 : right+1; > public static void main(String[] args) < HeightDepthBST a = new HeightDepthBST(); a.root = a.createBST(); System.out.println("Height "+height(a.root)); System.out.println("Depth "+depth(a.root)); > Node createBST() < // Tree 4 in above root = null; root = add (root, 12); root = add (root, 6); root = add (root, 5); root = add (root, 8); root = add (root, 7); root = add (root, 9); root = add (root, 14); root = add (root, 18); root = add (root, 16); return root; > Node add (Node node, int data) < if (null == node) return new Node (data); else if (data < node.data) node.left = add (node.left, data); else if (data > node.data) node.right = add (node.right, data); return node; > > class Node < int data; Node left, right; Node (int data) < this.data=data; > > Временная сложность кода height() и depth() составляет O(N).
Вывод
В этой статье мы проследили 2 важных свойства бинарного дерева, а именно высоту и глубину. Мы посетили код, чтобы вычислить их. Мы также увидели, в чем разница между ними с точки зрения дерева.
Источник
Деревья
Дерево — это нелинейная иерархическая структура данных. Она состоит из узлов и ребер, которые соединяют узлы.
Зачем нужны деревья
Другие структуры данных, например, массивы, списки, стеки и очереди, линейные. Это значит, что данные в них хранятся последовательно. Когда мы выполняем любую операцию в линейной структуре данных, временная сложность растет с увеличением размера данных. В современном мире это не очень круто.
Разные древовидные структуры позволяют быстрее и легче получать доступ к данным, поскольку дерево — структура нелинейная.
Части дерева
- Узел — это объект, в котором есть ключ или значение и указатели на дочерние узлы.
Узлы, у которых нет дочерних узлов, называют листами или терминальными узлами.
Узлы, у которых есть хотя бы один дочерний узел, называются внутренними. - Ребро связывает два узла.
- Корень — это самый верхний узел дерева. Его ещё иногда называют корневым узлом.
.png)
Другие понятия
- Высота узла — это максимальная длина пути от этого узла к самому нижнему узлу (листу).
- Глубина вложенности узла — длина пути от корня до этого узла.
- Высота дерева — это высота корневого узла или глубина самого глубокого узла.
- Степень узла — это общее количество ребер, которые соединены с этим узлом.
- Лес — множество непересекающихся деревьев. Например, если «срезать» корень, получится лес.
Виды деревьев
Обход дерева
Чтобы выполнить какую-либо операцию с деревом, нужно добраться до определенного узла. Для этого и существуют алгоритмы обхода дерева. Они помогают «дойти» до необходимого узла.
Где используются
- Деревья двоичного поиска помогают быстро проверить наличие элемента в наборе.
- Куча — это тоже своеобразное дерево. Кучи используют в алгоритме сортировки кучей.
- Префиксные деревья используются в маршрутизаторах, они хранят информацию о маршруте.
- Большинство популярных баз данных основаны на B-деревья и T-деревья.
- Компиляторы используют абстрактное синтаксическое дерево, чтобы находить синтаксические ошибки в ваших программах.
СodeСhick.io — простой и эффективный способ изучения программирования.
2023 © ООО «Алгоритмы и практика»
Источник