Ориентированные и бинарные деревья. Определения
Ориентированное дерево (корневое ориентированное дерево) (рисунок 6.76) – это ориентированный граф без циклов со свойствами:
1. Существует в точности одна вершина , называемая корнем, в которую не заходит ни одна дуга.
2. В каждую вершину, кроме корня, заходит в точности одна дуга.
3. Существует путь из корня в любую другую вершину.
Потомок вершины – это вершина , в которую ведет путь из вершины ; при этом называется предком для . Если длина этого пути равна 1, то есть из в ведет дуга, то – «отец» для , а – «сын» для .
Вершины, у которых общий отец, называются братьями или сестрами.
Вершина, не имеющая потомков, называется листом.
Глубина вершины в дереве – это длина пути из корня в .
Высота вершины в дереве – это длина самого длинного пути из в какой-нибудь лист.
Высота дерева – это число дуг самого длинного пути, то есть высота корня.
Уровень вершины – это разность между высотой всего дерева и глубиной вершины .
Высота дерева на рисунке 6.77 равна 3, вершина 8 имеет глубину 2, высоту 1, уровень 1.
Лемма. Если в любом неориентированном дереве выбрать произвольную вершину в качестве корня и сориентировать все ребра в направлении «от корня», т.е. сделать началом всех инцидентных ей ребер, вершины, смежные с – началами всех инцидентных им еще не сориентированных ребер и т.д., то полученный в результате ориентированный граф будет ориентированным деревом.
Упорядоченное ориентированное дерево – это дерево, у которого множество сыновей каждой вершины упорядочено, обычно слева направо, как на рисунке 62: .
Бинарное (двоичное) дерево – это упорядоченное дерево, из каждой вершины которого может исходить не более двух дуг. Ориентированное дерево называют бинарным, если полустепень исхода любой его вершины не больше 2.
Бинарное ориентированное дерево называют полным, если из любой его вершины, не являющейся листом, исходят ровно две дуги, а уровни всех листьев совпадают.
Каждая вершина бинарного дерева может иметь либо двух сыновей – левого и правого (вершина 2 имеет левого сына 3 и правого сына 4), либо иметь только левого сына (левый сын 9 вершины 8), либо только правого сына (вершина 5 – единственный правый сын вершины 4), либо не иметь ни одного сына (листья 3, 5, 7, 9).
Бинарное дерево называется полным, если у каждой его внутренней вершины имеется два сына и все его ветви имеют одинаковую длину.
Полное бинарное дерево уровня – это дерево, в котором каждый узел уровня является листом и каждый узел уровня меньше имеет непустые левое и правое поддеревья.
На рисунке 6.78 приведен пример полного бинарного дерева уровня 3.
Левое поддерево вершины – это максимальное поддерево, корнем которого является левый сын вершины .
Правое поддерево вершины – это максимальное поддерево, корнем которого является правый сын вершины .
На рисунке 6.77 левое поддерево вершины 6 состоит из одной вершины 7, правое поддерево – из вершин 8, 9 и дуги (8,9).
Теорема 6.13 (теорема о высоте бинарного ориентированного дерева с заданным числом листьев). Бинарное ориентированное дерево с листьями имеет высоту, не меньшую .
Источник
4.5. Деревья
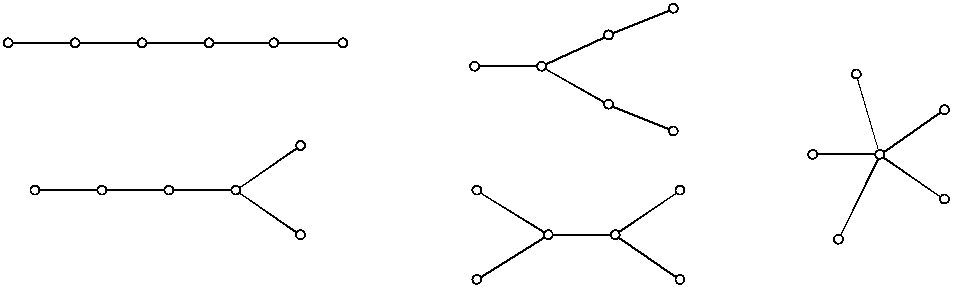
В особый тип графов выделяются деревья. Дерево – это связанный граф , не имеющий циклов, так как любые две его вершины соединены простым путем. На рис. 4.14 показаны все пять видов деревьев, которые могут быть получены на шести вершинах.
Ориентированным деревом называется бесконтурный орграф, у которого отрицательная полустепень ρ – любой вершины не более 1 и существует ровно одна вершина, называемая корнем ориентированного дерева, у которой отрицательная степень ρ – = 0.
Опираясь на данное определение, можно доказать, что в ориентированном дереве любая вершина достижима из корня.
Для ориентированных деревьев свойства 1 и 3 верны всегда, а свойство 2 – нет. Вот почему ориентированное дерево: 1) всегда слабо связно; 2) односторонне связно, только если оно является ориентированной цепью (т.е. когда все вершины лежат на единственном пути из корня); 3) никогда не бывает сильносвязным, поскольку сильно связный граф обязательно содержит цикл.
Для всех вершин ориентированного дерева, за исключением корня, отрицательная полустепень ρ – = 1, а положительная полустепень ρ + может принимать любое значение от нуля. При этом те вершины, у которых положительная полустепень ρ + = 0, называются листьями дерева. Ориентированное дерево, у которого каждая вершина, отличная от корня, есть лист, называется кустом.
Рассмотрим некоторые параметры, которые характеризуют ориентированное дерево.
v0 Уровень 3
v1 v2 v3 Уровень 2
v4 v5 v6 v7 v8 Уровень 1
v9 Уровень 0
Высота ориентированного дерева – это наибольшая длина пути из корня в лист; глубина вершины ориентированного дерева – это длина пути из корня в эту вершину; высота вершины – это наибольшая длина пути из данной вершины в лист и , наконец, уровень вершины ориентированного дерева – это разность между высотой ориентированного дерева и глубиной данной вершины. Из этих определений можно сделать вывод, что уровень корня равен высоте дерева, но уровни различных листьев так же, как и их глубины, могут быть различны, однако высота любого листа равна нулю (рис. 4.15).
В заключение этой главы следует еще раз отметить, что графы являются одним из наиболее распространенных языков для представления разнообразных математических объектов и формулировки различных теоретических и прикладных задач, выходящих за пределы собственно теории графов. Трудно назвать прикладную область, где не применяется теория графов. Графы используются в математической логике и теории формальных систем, в теории алгоритмов и теоретическом программировании (для представления и анализа алгоритмов и программ), в теории языков и грамматик (для синтаксического анализа текстов). Они используются для описания и анализа как статических структур (организационных структур, транспортных сетей), так и динамических систем, в которых вершинам соответствуют состояния системы, а ориентированным ребрам – переходы из одного состояния в другое. Именно графы являются наиболее удобным средством формализованного представления конечных автоматов.
1. Сколько существует неориентированных графов с n вершинами?
2. Доказать, что сумма степеней всех вершин неориентированного графа равна удвоенному числу ребер ( это утверждение известно под названием «леммы о рукопожатиях»).
3. Установить, какие из изображенных на рис. 4.19 графов изоморфны, а какие нет
4. Найти все попарно неизоморфные графы неориентированные графы с четырьмя вершинами и тремя ребрами.
5. Установить, является ли ориентированный граф, изображенный на рис. 4.20, связным. Постройте матрицу смежности для этого графа.
6. Доказать, что связный неориентированный граф имеет эйлеров цикл тогда и только тогда, когда степень каждой его вершины четная. Рис. 4. 20
7. Инцидентор графа Р определен значениями: P(a,1,b); P(b,2,b); P(b,3,с); P(е,4,b); P(c,5,d); P(d,6,с); P(f,7,c); P(d,8, d); P(е,9,d); P(a,10,е); P(а,11,d); P(a,12,f) – которые истинны, остальные ложны. Построить граф, составить таблицы смежности и инцидентности, определить центр графа.
8. Ориентированный граф задан матрицей смежности, содержащей метки соответствующих ребер: построить граф и решить задачу о кратчайших путях.
0 7 8 9 10
9. Доказать, что ориентированный граф связный тогда и только тогда, когда в нем есть путь, проходящий через все вершины. Останется ли это утверждение справедливым, если потребовать, чтобы существовал простой путь.
10. Вычислите количество деревьев на множестве р вершин при р = 5;10;15;20. Сколько времени потребовалось бы для подсчета деревьев с производительностью 10 6 операций/с, считая одну операцию на дерево?
Источник
4.5. Деревья
В особый тип графов выделяются деревья. Дерево – это связанный граф , не имеющий циклов, так как любые две его вершины соединены простым путем. На рис. 4.14 показаны все пять видов деревьев, которые могут быть получены на шести вершинах.
Ориентированным деревом называется бесконтурный орграф, у которого отрицательная полустепень ρ – любой вершины не более 1 и существует ровно одна вершина, называемая корнем ориентированного дерева, у которой отрицательная степень ρ – = 0.
Опираясь на данное определение, можно доказать, что в ориентированном дереве любая вершина достижима из корня.
Для ориентированных деревьев свойства 1 и 3 верны всегда, а свойство 2 – нет. Вот почему ориентированное дерево: 1) всегда слабо связно; 2) односторонне связно, только если оно является ориентированной цепью (т.е. когда все вершины лежат на единственном пути из корня); 3) никогда не бывает сильносвязным, поскольку сильно связный граф обязательно содержит цикл.
Для всех вершин ориентированного дерева, за исключением корня, отрицательная полустепень ρ – = 1, а положительная полустепень ρ + может принимать любое значение от нуля. При этом те вершины, у которых положительная полустепень ρ + = 0, называются листьями дерева. Ориентированное дерево, у которого каждая вершина, отличная от корня, есть лист, называется кустом.
Рассмотрим некоторые параметры, которые характеризуют ориентированное дерево.
v0 Уровень 3
v1 v2 v3 Уровень 2
v4 v5 v6 v7 v8 Уровень 1
v9 Уровень 0
Высота ориентированного дерева – это наибольшая длина пути из корня в лист; глубина вершины ориентированного дерева – это длина пути из корня в эту вершину; высота вершины – это наибольшая длина пути из данной вершины в лист и , наконец, уровень вершины ориентированного дерева – это разность между высотой ориентированного дерева и глубиной данной вершины. Из этих определений можно сделать вывод, что уровень корня равен высоте дерева, но уровни различных листьев так же, как и их глубины, могут быть различны, однако высота любого листа равна нулю (рис. 4.15).
В заключение этой главы следует еще раз отметить, что графы являются одним из наиболее распространенных языков для представления разнообразных математических объектов и формулировки различных теоретических и прикладных задач, выходящих за пределы собственно теории графов. Трудно назвать прикладную область, где не применяется теория графов. Графы используются в математической логике и теории формальных систем, в теории алгоритмов и теоретическом программировании (для представления и анализа алгоритмов и программ), в теории языков и грамматик (для синтаксического анализа текстов). Они используются для описания и анализа как статических структур (организационных структур, транспортных сетей), так и динамических систем, в которых вершинам соответствуют состояния системы, а ориентированным ребрам – переходы из одного состояния в другое. Именно графы являются наиболее удобным средством формализованного представления конечных автоматов.
1. Сколько существует неориентированных графов с n вершинами?
2. Доказать, что сумма степеней всех вершин неориентированного графа равна удвоенному числу ребер ( это утверждение известно под названием «леммы о рукопожатиях»).
3. Установить, какие из изображенных на рис. 4.19 графов изоморфны, а какие нет
4. Найти все попарно неизоморфные графы неориентированные графы с четырьмя вершинами и тремя ребрами.
5. Установить, является ли ориентированный граф, изображенный на рис. 4.20, связным. Постройте матрицу смежности для этого графа.
6. Доказать, что связный неориентированный граф имеет эйлеров цикл тогда и только тогда, когда степень каждой его вершины четная. Рис. 4. 20
7. Инцидентор графа Р определен значениями: P(a,1,b); P(b,2,b); P(b,3,с); P(е,4,b); P(c,5,d); P(d,6,с); P(f,7,c); P(d,8, d); P(е,9,d); P(a,10,е); P(а,11,d); P(a,12,f) – которые истинны, остальные ложны. Построить граф, составить таблицы смежности и инцидентности, определить центр графа.
8. Ориентированный граф задан матрицей смежности, содержащей метки соответствующих ребер: построить граф и решить задачу о кратчайших путях.
0 7 8 9 10
9. Доказать, что ориентированный граф связный тогда и только тогда, когда в нем есть путь, проходящий через все вершины. Останется ли это утверждение справедливым, если потребовать, чтобы существовал простой путь.
10. Вычислите количество деревьев на множестве р вершин при р = 5;10;15;20. Сколько времени потребовалось бы для подсчета деревьев с производительностью 10 6 операций/с, считая одну операцию на дерево?
Источник