3.9. Деревья и леса
Каждая компонента связности леса – дерево, следовательно, для 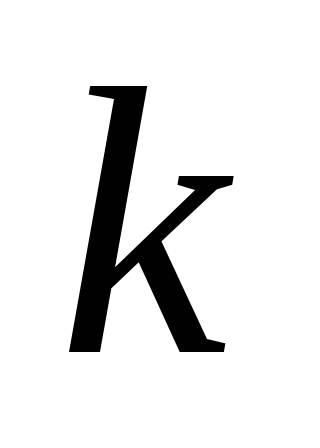

П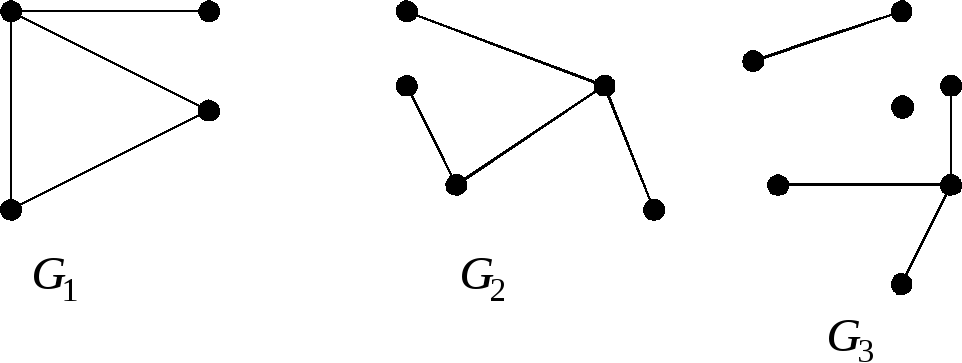


Лемма. Если граф – дерево, то каждое его ребро является мостом.
Доказательство.В параграфе 3.6 было доказано, что если ребро графа не содержится ни в одном цикле, то оно является мостом. Дерево граф ациклический, следовательно, каждое его ребро мост.■
Теорема (основная теорема о деревьях). Для графа следующие утверждения равносильны:
- Граф
— дерево.
ациклический и
.
связный и
.
связный и каждое его ребро является мостом.
- Любые две вершины графа
можно соединить, притом единственной, простой цепью.
ациклический, и добавление к нему нового ребра приводит к образованию единственного простого цикла.
Доказательство.Доказательство проведем по следующей схеме:


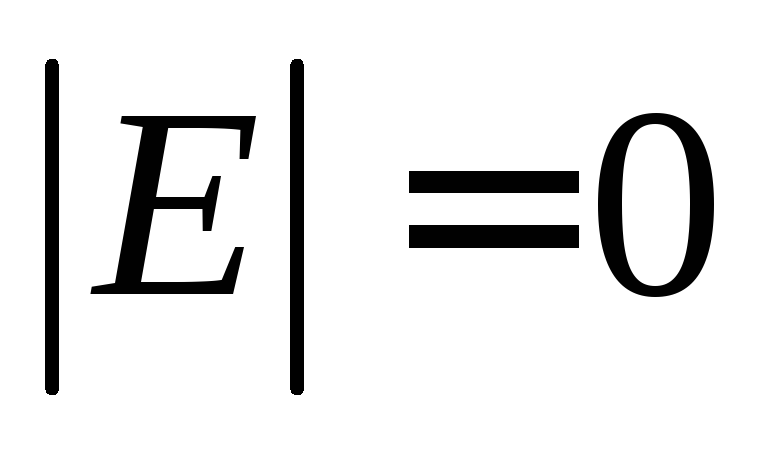
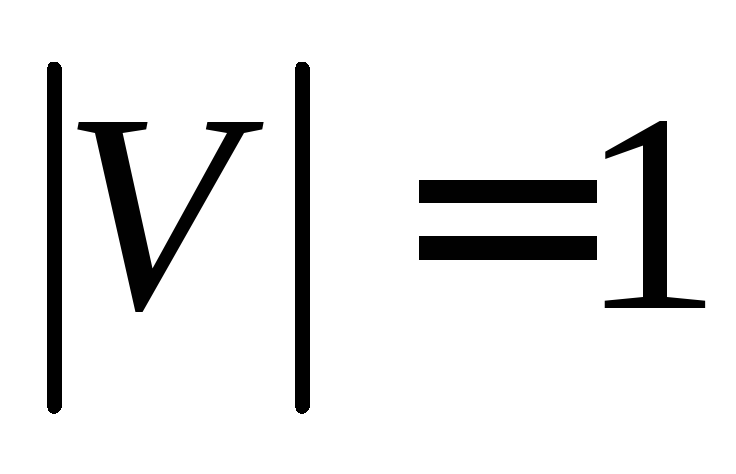
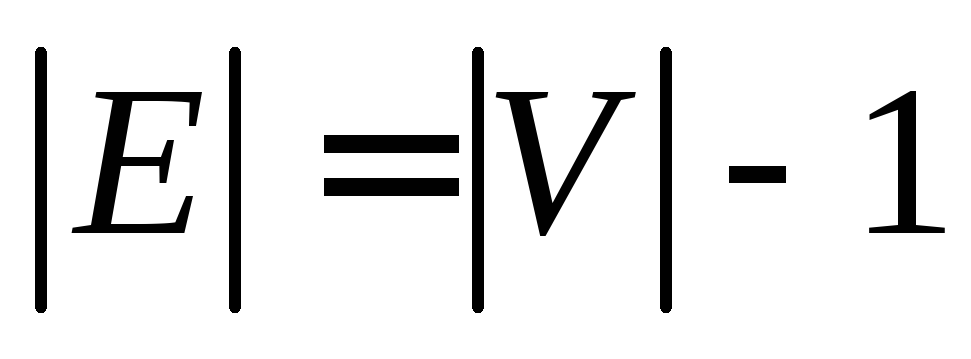




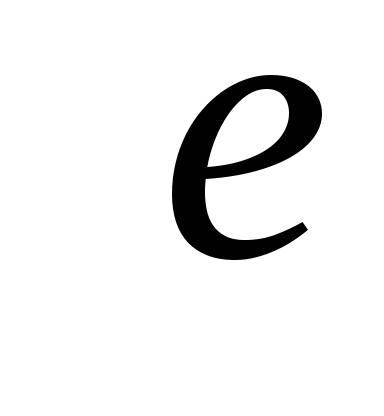
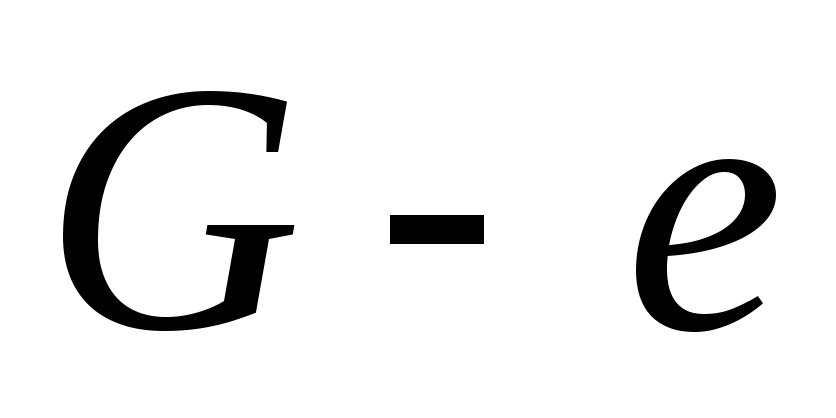
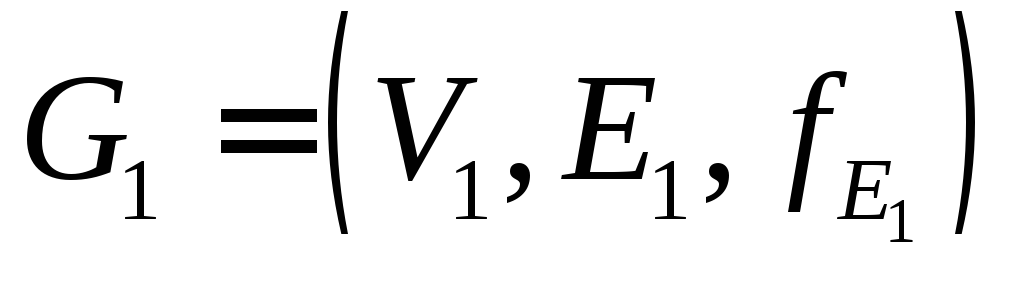
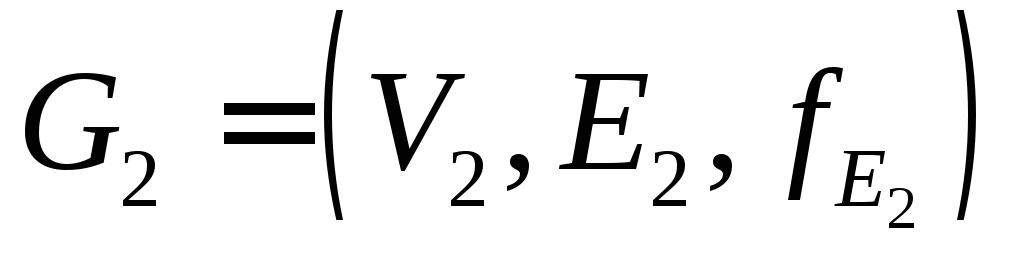
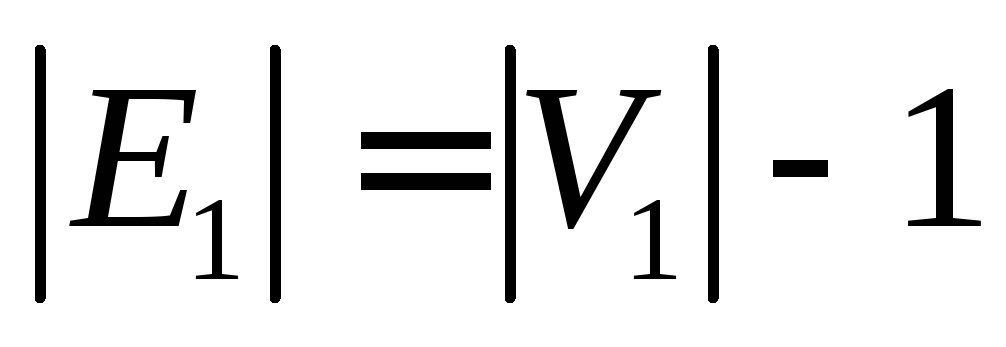
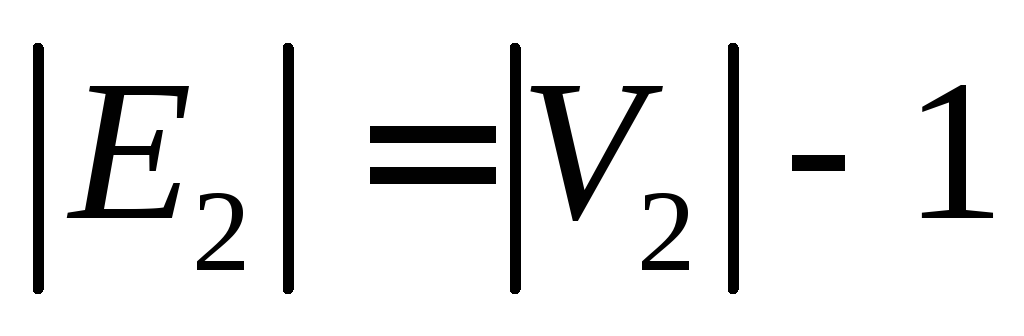



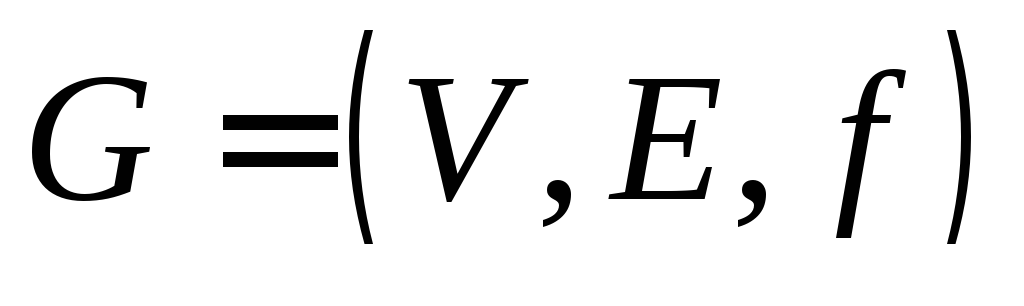
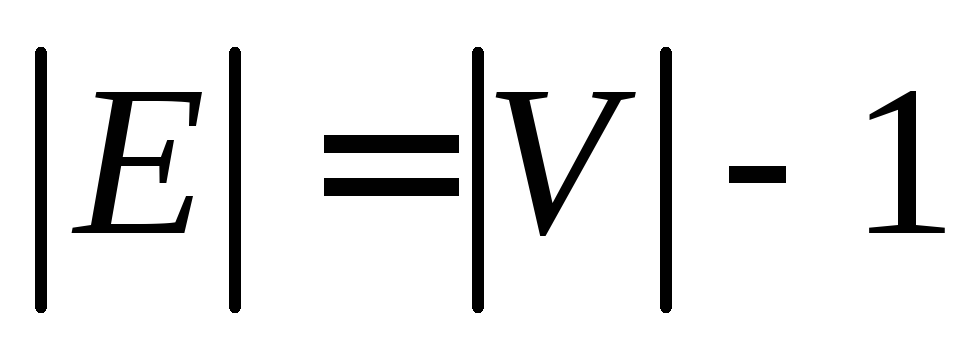

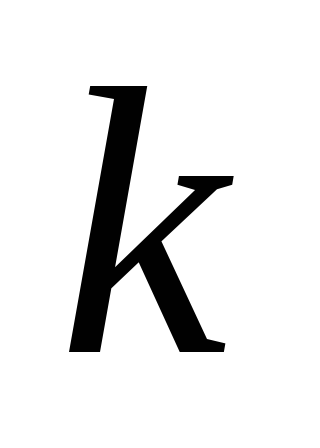











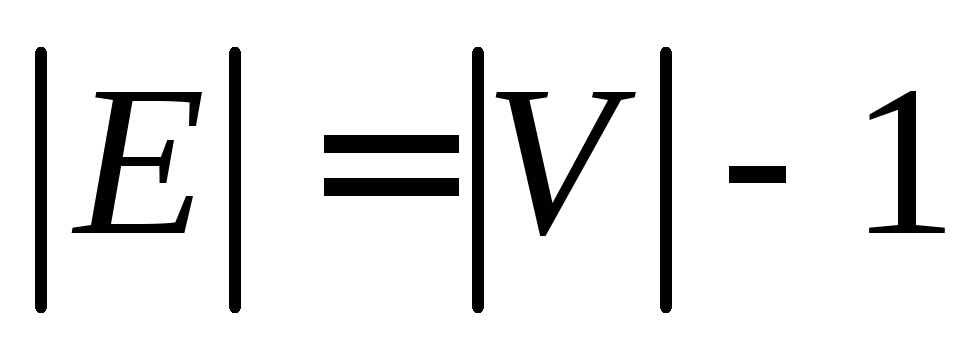



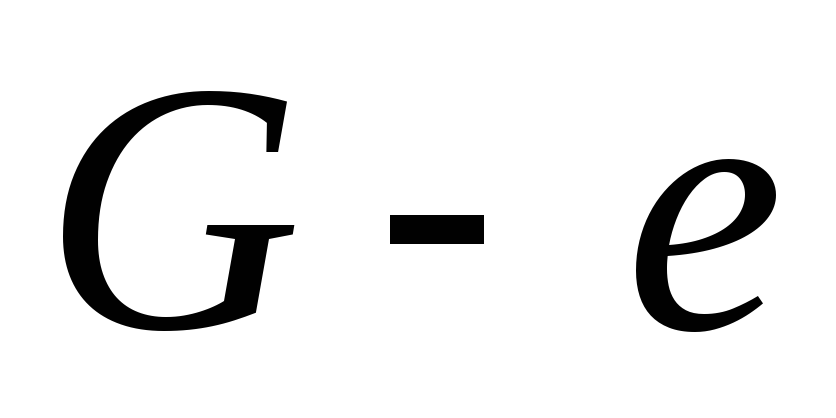
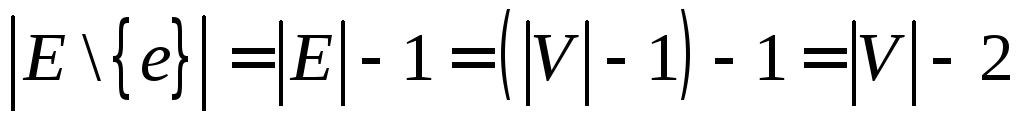
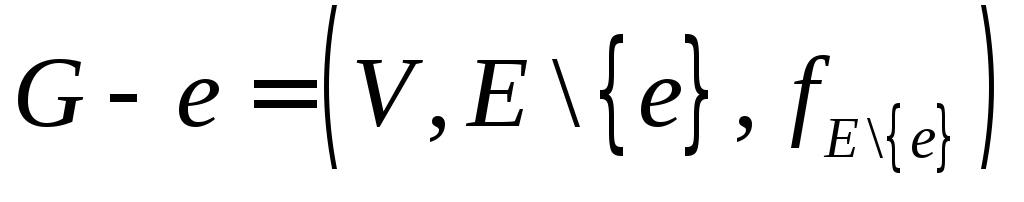











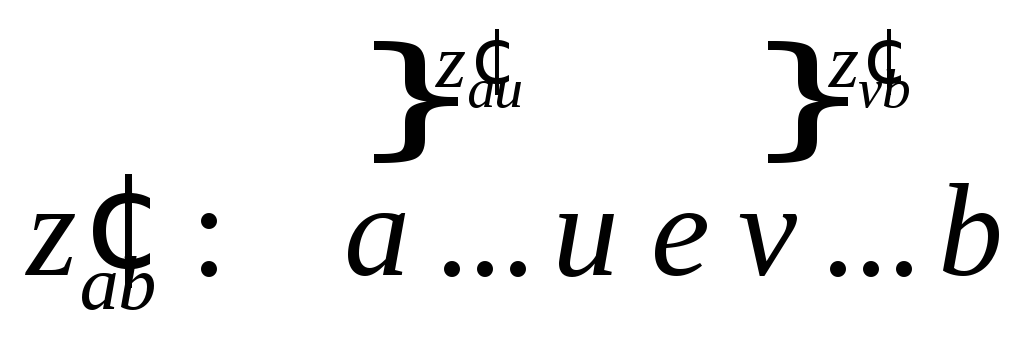



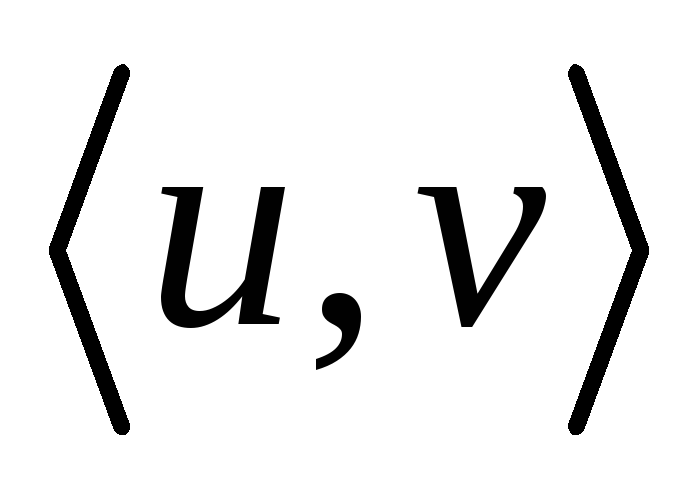

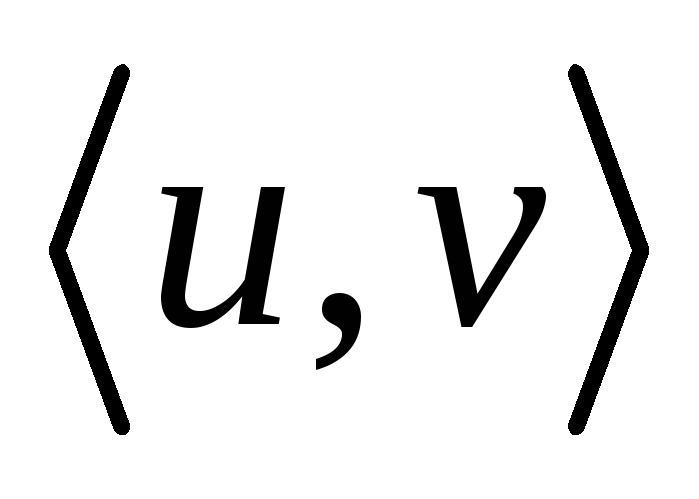
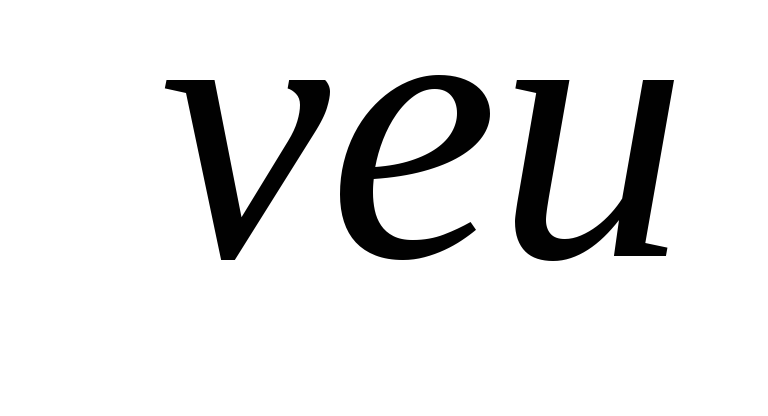

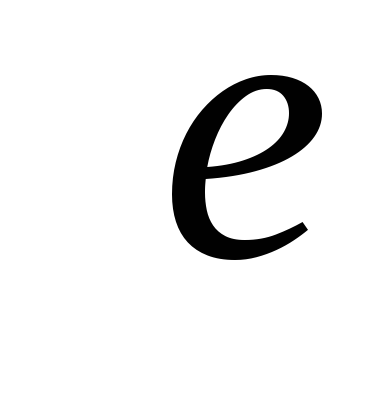






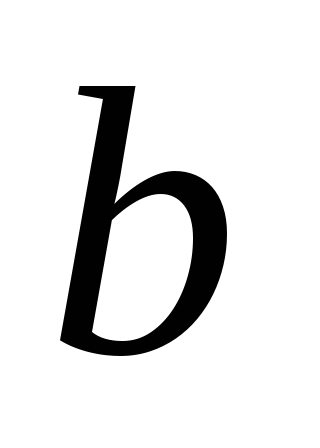







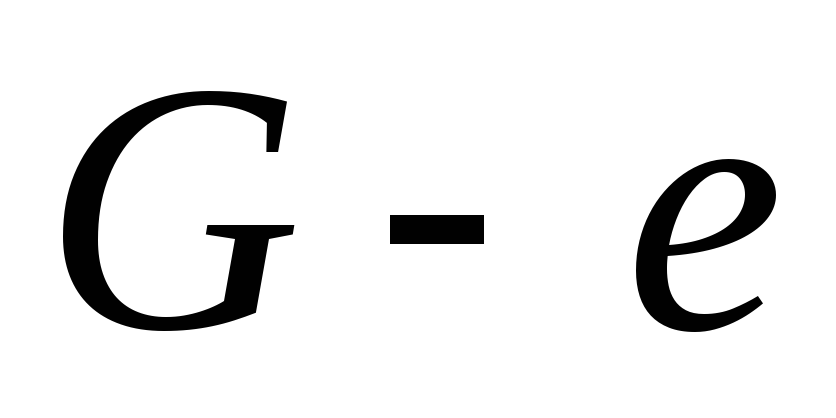

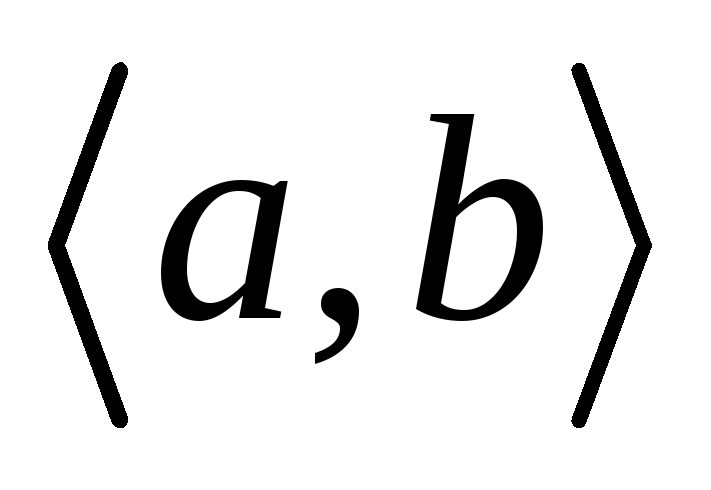



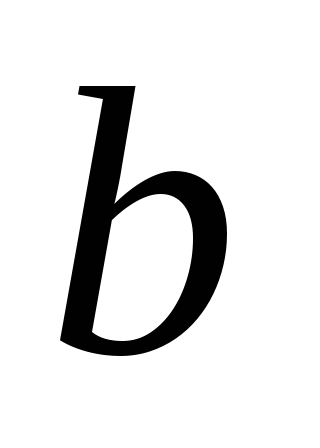





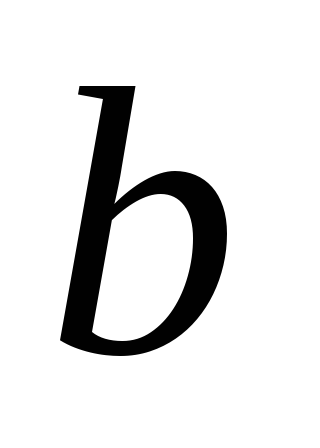
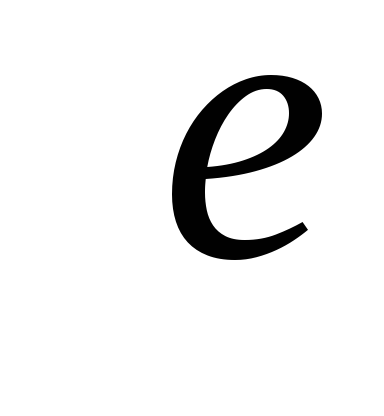
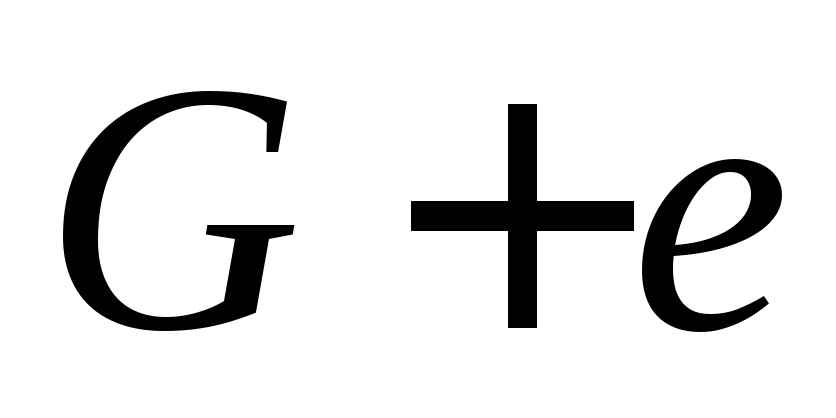

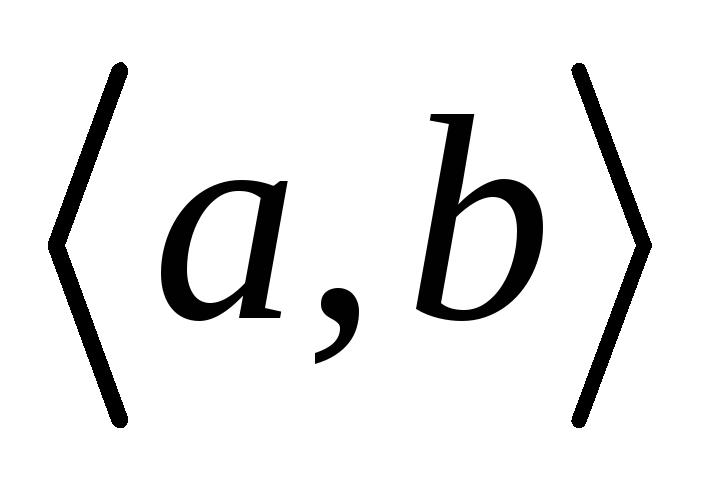

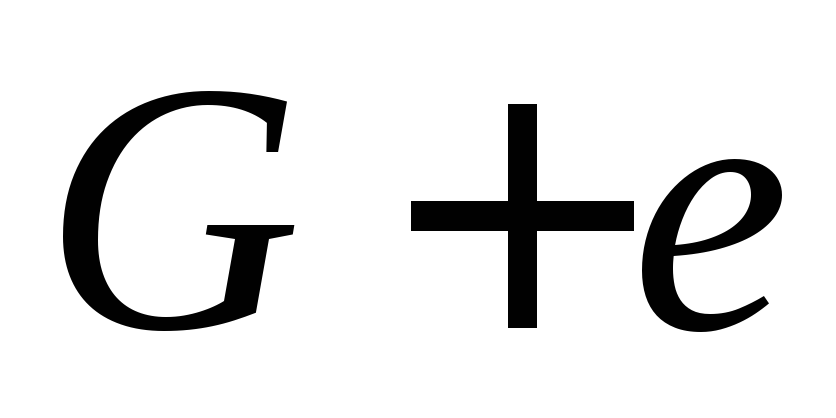

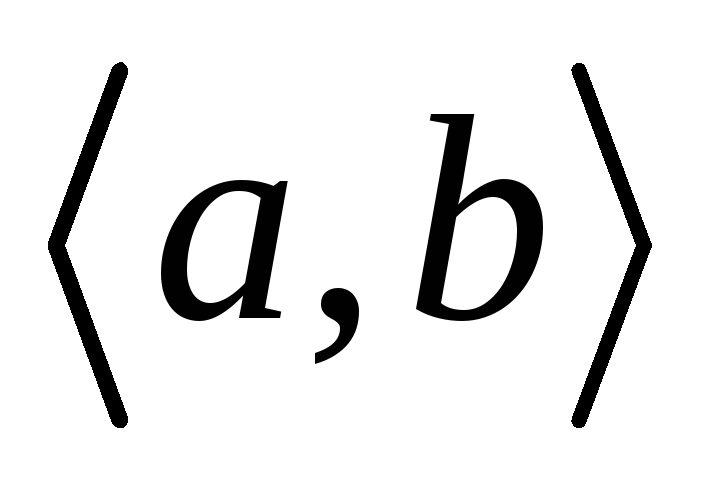




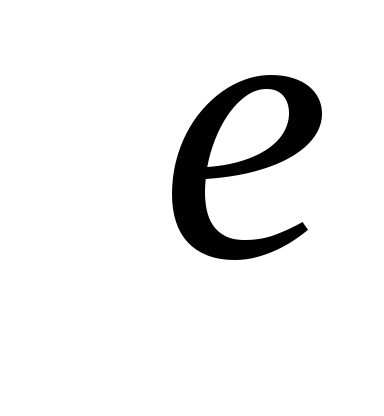








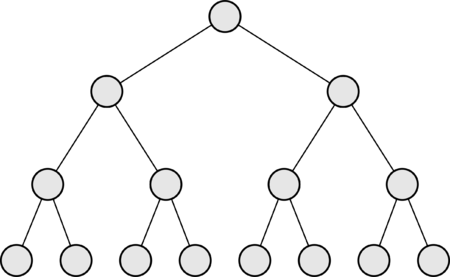
Источник
Дерево, эквивалентные определения
Для графа [math]G[/math] эквивалентны следующие утверждения:
- [math]G[/math] — дерево.
- Любые две вершины графа [math]G[/math] соединены единственным простым путем.
- [math]G[/math] — связен и [math] p = q + 1 [/math] , где [math]p[/math] — количество вершин, а [math]q[/math] количество ребер.
- [math]G[/math] — ацикличен и [math] p = q + 1 [/math] , где [math]p[/math] — количество вершин, а [math]q[/math] количество ребер.
- [math]G[/math] — ацикличен и при добавлении любого ребра для несмежных вершин появляется один простой цикл.
- [math]G[/math] — связный граф, отличный от [math] K_p [/math] для [math] p \gt 3 [/math] , а также при добавлении любого ребра для несмежных вершин появляется один простой цикл.
- [math]G[/math] — граф, отличный от [math] K_3 \cup K_1 [/math] и [math] K_3 \cup K_2 [/math] , а также [math] p = q + 1 [/math] , где [math]p[/math] — количество вершин, а [math]q[/math] количество ребер, и при добавлении любого ребра для несмежных вершин появляется один простой цикл.
Доказательство эквивалентности
Граф связен, поэтому любые две вершнины соединены путем. Граф ацикличен, значит путь единственен, а также прост, поскольку никакой путь не может зайти в одну вершину два раза, потому что это противоречит ацикличности.
Очевидно, что граф связен. Докажем по индукции, соотношение [math]p = q + 1[/math] . Утверждение очевидно для связных графов с одной и двумя вершинами. Предположим, что оно верно для графов, имеющих меньше [math]p[/math] вершин. Если же граф [math]G[/math] имеет [math]p[/math] вершин, то удаление из него любого ребра делает граф [math] G [/math] несвязным в силу единственности простых цепей; более того, получаемый граф будет иметь в точности две компоненты. По предположению индукции в каждой компоненте число вершин на единицу больше числа ребер. Таким образом, [math] p = q + 1 [/math] .
Очевидно, что если граф связен и ребер на одно меньше, чем вершин, то он ацикличен. Преположим, что у нас есть p вершин, и мы добавляем ребра. Если мы добавили ребро для получения цикла, то добавили второй путь между парой вершин, а значит нам не хватит его на добавление вершины и мы получим не связный граф, что противоречит условию.
[math]G[/math] — ациклический граф, значит каждая компонента связности графа является деревом. Так как в каждой из них вершин на единицу больше чем ребер, то [math] p = q + k [/math] , где [math]k[/math] — число компонент связности. Поскольку [math] p = q + k [/math] , то [math] k = 1 [/math] , а значит [math]G[/math] — связен. Таким образом наш граф — дерево, у которого между любой парой вершин есть единственный простой путь. Очевидно, при добавлении ребра появится второй путь между парой вершин, то есть мы получим цикл.
Поскольку [math] K_p [/math] для [math] p \gt 3 [/math] содержит простой цикл, то [math]G[/math] не может им являться. [math]G[/math] связен, так как в ином случае можно было бы добавить ребро так, что граф остался бы ациклическим.
Докажем, что любые две вершины графа соединены единственной простой цепью, а тогда поскольку [math] 2 \Rightarrow 3 [/math] , получим [math] p = q + 1 [/math] . Любые две вершины соединены простой цепью, так как [math]G[/math] — связен. Если две вершины соединены более чем одной простой цепью, то мы получим цикл. Причем он должен являться [math] K_3 [/math] , так как иначе добавив ребро, соединяющее две вершины цикла, мы получим более одного простого цикла, что противоречит условию. [math] K_3 [/math] является собственным подграфом [math]G[/math] , поскольку [math]G[/math] не является [math] K_p [/math] для [math] p \gt 3 [/math] . [math]G[/math] — связен, а значит есть вершина смежная с [math] K_3 [/math] . Очевидно, можно добавить ребро так, что образуется более одного простого цикла. Если нельзя добавить ребра так, чтобы не нарушалось исходное условие, то граф [math]G[/math] является [math]K_p[/math] для [math] p \gt 3 [/math] , и мы получаем противоречие с исходным условием. Значит, любые две вершины графа соединены единственной простой цепью, что и требовалось.
Если [math]G[/math] имеет простой цикл, то он является отдельной компонентой [math]K_3[/math] по ранее доказанному. Все остальные компоненты должны быть деревьями, но для выполнения соотношения [math] p = q + 1 [/math] должно быть не более одной компоненты отличной от [math]K_3[/math] , так как в [math]K_3[/math] [math] p = q = 3 [/math] . Если это дерево содержит простой путь длины 2, то в [math]G[/math] можно добавить ребро так, что образуются два простых цикла. Следовательно, этим деревом является [math]K_1[/math] или [math]K_2[/math] . Значит [math]G[/math] является [math]K_3 \cup K_1[/math] или [math]K_3 \cup K_2[/math] , которые мы исключили из рассмотрения. Значит наш граф ацикличен. Если [math]G[/math] ациклический и [math] p = q + 1 [/math] , то из [math] 4 \Rightarrow 5 [/math] и [math] 5 \Rightarrow 6 [/math] верно, что [math]G[/math] — связен. В итоге получаем, что [math]G[/math] является деревом по определению.
См. также
Источники информации
- Харари Ф. Теория графов. /пер. с англ. — изд. 2-е — М.: Едиториал УРСС, 2003. — 296 с. — ISBN 5-354-00301-6
- Википедия — дерево(теория графов)
Источник
Теория графов
Следующая теорема устанавливает, что два из четырех свойств – связность, ацикличность, древовидность и субцикличность – характеризуют граф как дерево.
- Для
– графа
следующие утверждения эквивалентны:
– дерево;
- Любые две несовпадающие вершины графа
соединяет единственная простая цепь;
– связный граф, и любое ребро есть мост;
– связный граф и древовидный;
– ациклический граф (лес) и древовидный;
– ациклический граф (лес) и субцикличекий;
– связный, субциклический и неполный,
;
– древовидный и субциклический, исключая
и
;
- (1->2): Если
-
Ориентированные деревья
- Ориентированным деревом (или ордеревом, или корневым деревом) называется орграф со следующими свойствами:
- существует единственный узел, в который не входит ни один другой узел. Он называется корнем ордерева;
- во все остальные узлы входит только по одному узлу;
- каждый узел достижим из корня.
- Ордерево обладает следующими свойствами:
- Концевая вершина ордерева называется листом. Путь из корня в лист называется ветвью. Длина наибольшей ветви ордерева называется высотой. Уровень узла ордерева – это расстояние отт корня до узла. Сам корень имеет уровень 0. Узлы одного уровня образуют ярус дерева.
 – дерево, то любые две его несовпадающие вершины соединяет единственная простая цепь. От противного. Пусть существуют две цепи
– дерево, то любые две его несовпадающие вершины соединяет единственная простая цепь. От противного. Пусть существуют две цепи 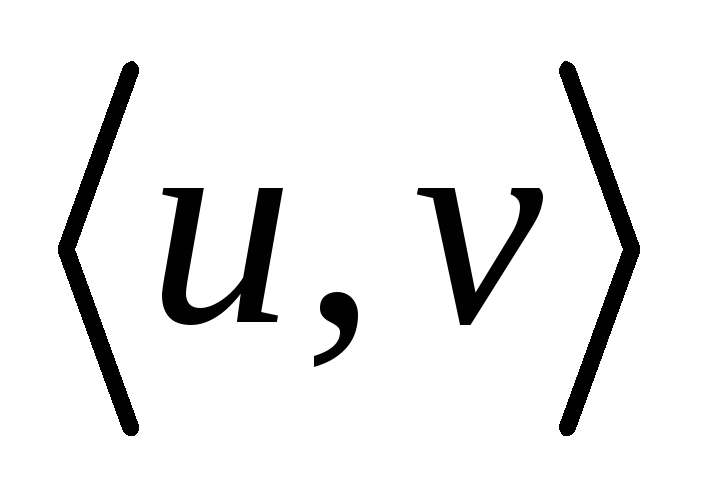 (см. рис.).
(см. рис.).  Тогда
Тогда 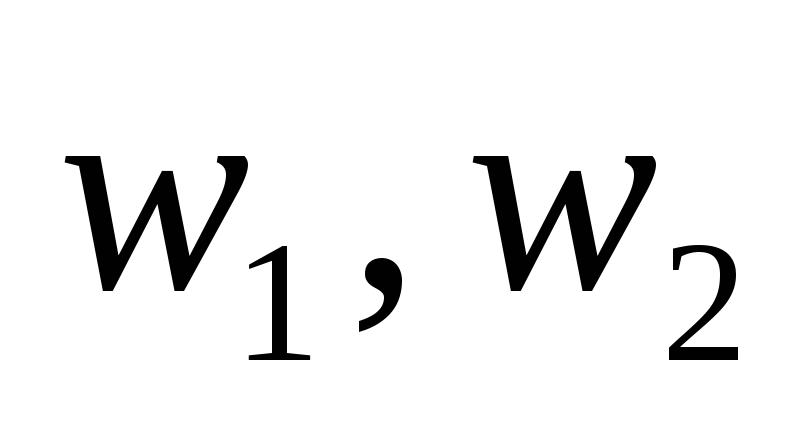 — простой цикл. (2->3): Если любые две несовпадающие вершины графа
— простой цикл. (2->3): Если любые две несовпадающие вершины графа  соединяет единственная простая цепь, то
соединяет единственная простая цепь, то  – связный граф, и любое ребро есть мост. Имеем:
– связный граф, и любое ребро есть мост. Имеем: 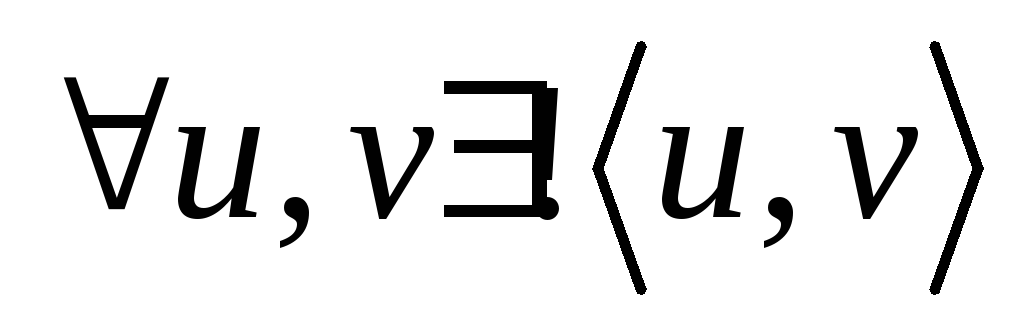

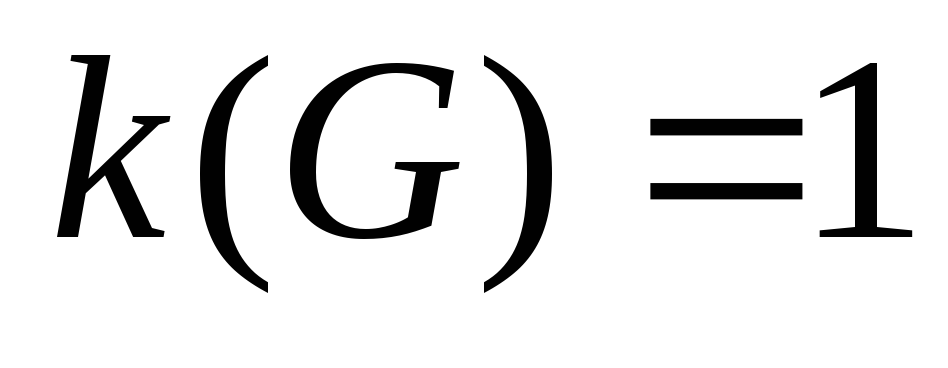 (число компонент связности). Далее от противного. Пусть ребро
(число компонент связности). Далее от противного. Пусть ребро 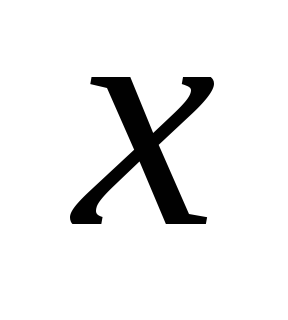 — не мост. Тогда в
— не мост. Тогда в 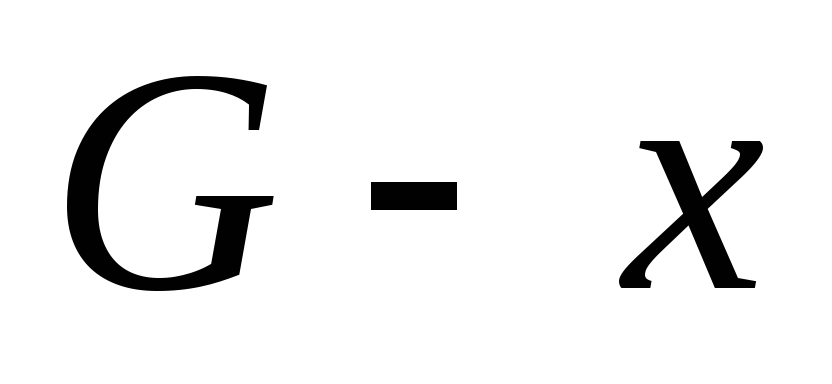 концы этого ребра связаны цепью. Само ребро
концы этого ребра связаны цепью. Само ребро 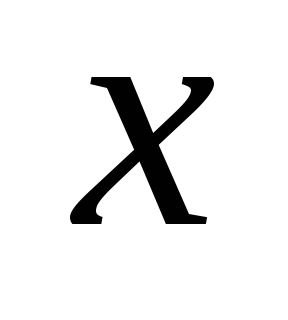 в исходном графе – вторая цепь, что противоречит условию. (3->4): Если
в исходном графе – вторая цепь, что противоречит условию. (3->4): Если  – связный граф, и любое ребро есть мост, то
– связный граф, и любое ребро есть мост, то  – связный и древовидный (
– связный и древовидный (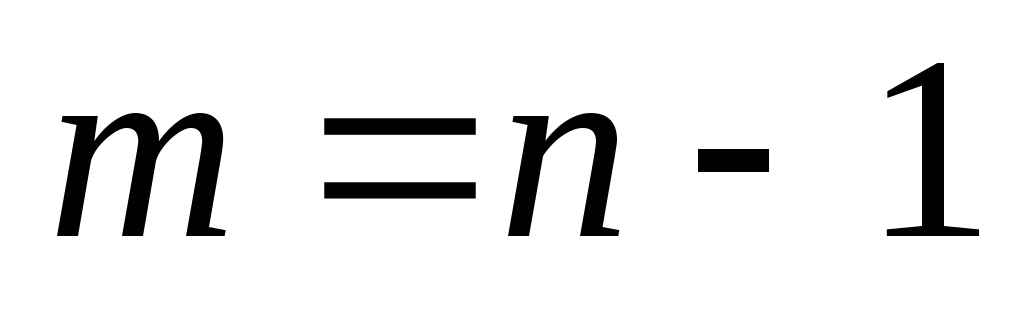 ). Индукция по
). Индукция по 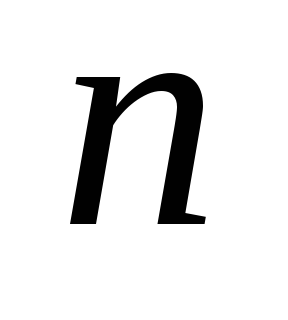 (числу вершин). Если
(числу вершин). Если 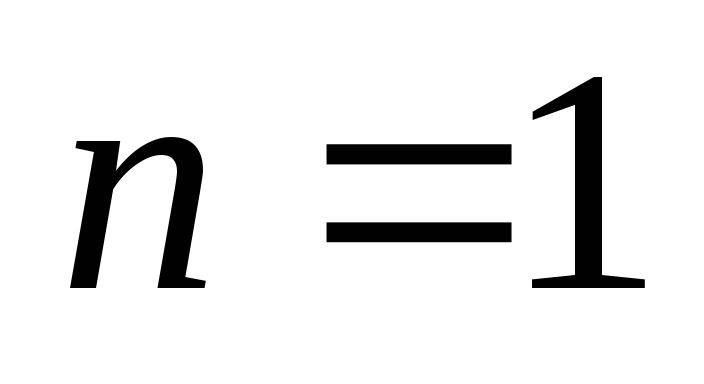 , то
, то 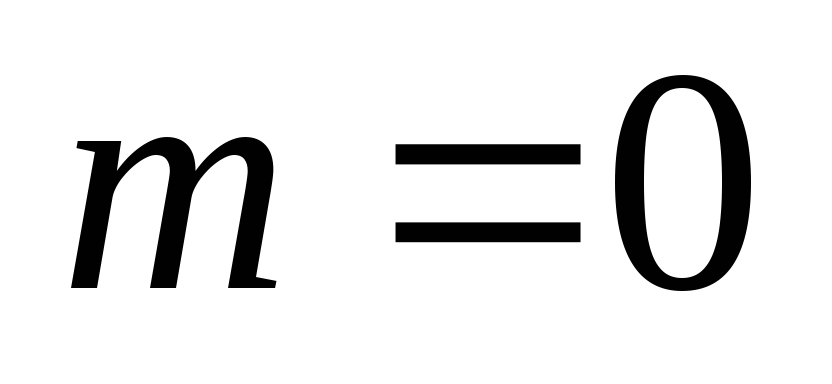 (число ребер). Пусть равенство
(число ребер). Пусть равенство 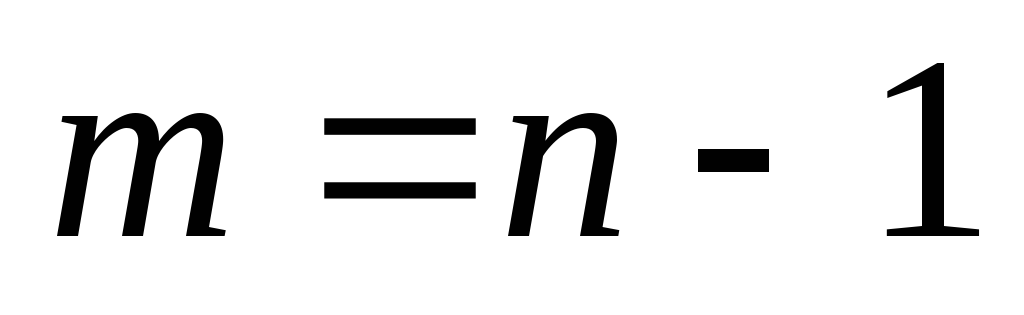 выполняется для всех графов
выполняется для всех графов  с числом вершин меньше
с числом вершин меньше 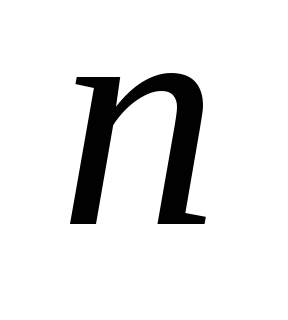 . Докажем, что оно выполняется и для
. Докажем, что оно выполняется и для 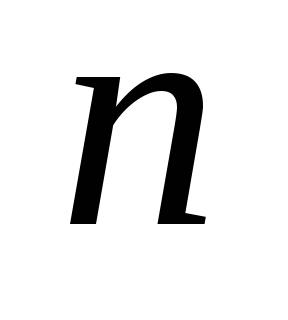 вершин. Удалим из
вершин. Удалим из  ребро
ребро 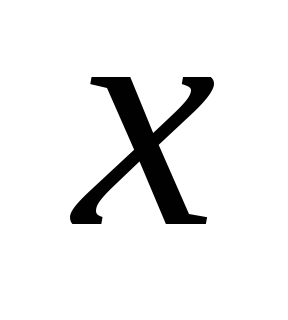 , являющееся мостом. Получим две компоненты связности
, являющееся мостом. Получим две компоненты связности  и
и  , для которых верно равенство
, для которых верно равенство 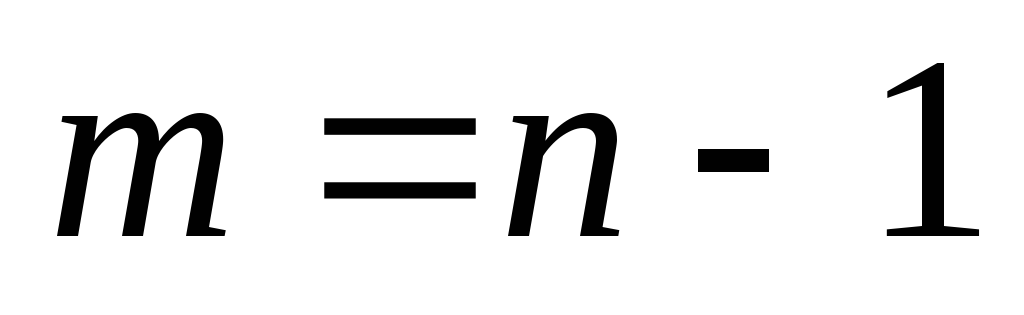 . Т.е.
. Т.е. 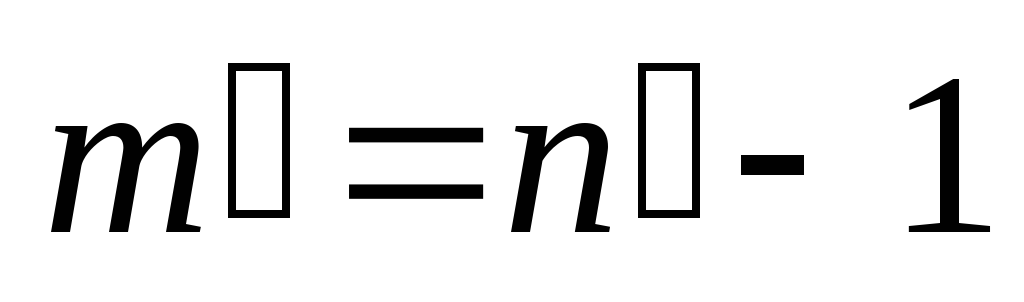 ,
, 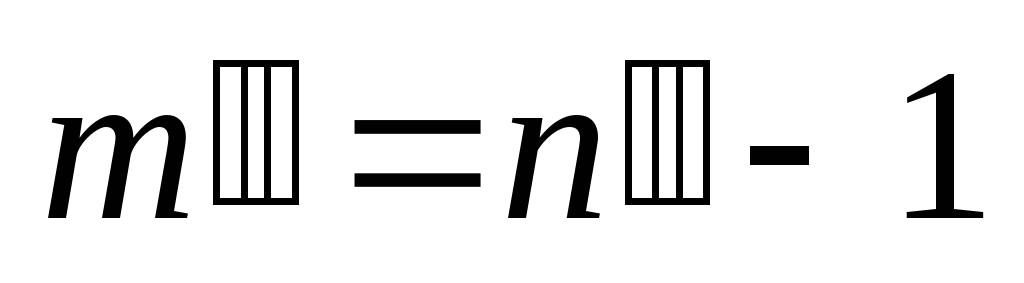 . Тогда
. Тогда  . (4->5): Если
. (4->5): Если  – связный и древовидный (
– связный и древовидный (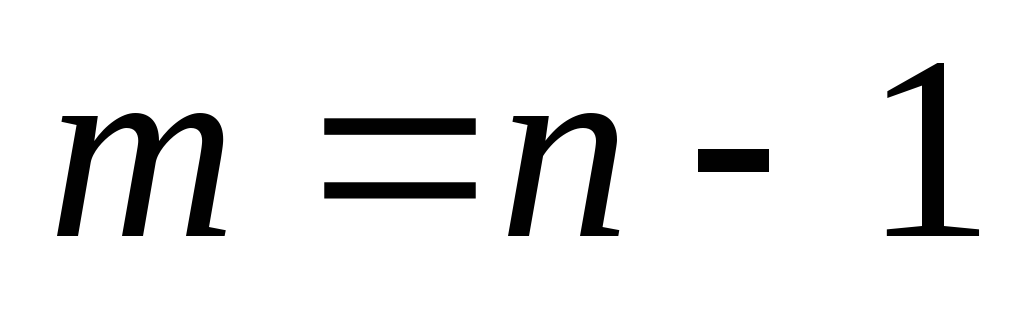 ), то
), то  – ациклический граф (лес) и древовидный (
– ациклический граф (лес) и древовидный (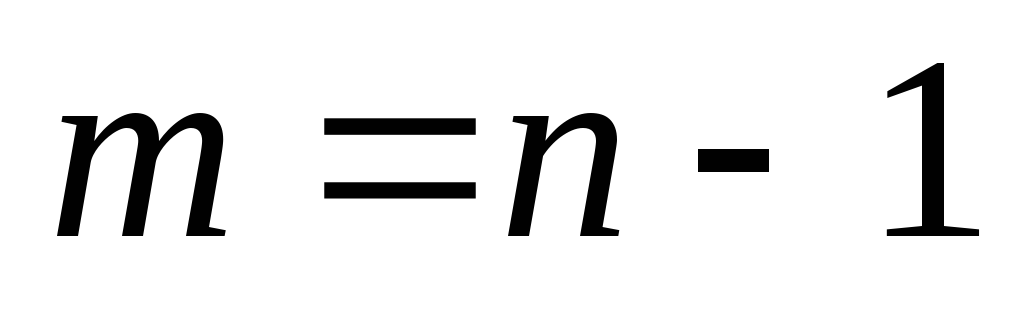 ). От противного. Пусть есть цикл с
). От противного. Пусть есть цикл с 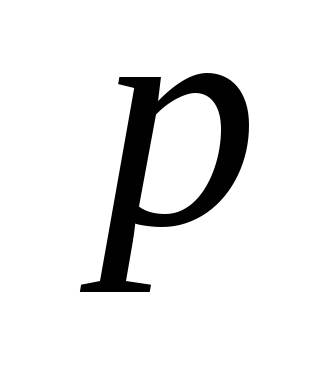 вершинами и
вершинами и  ребрами. Остальные
ребрами. Остальные 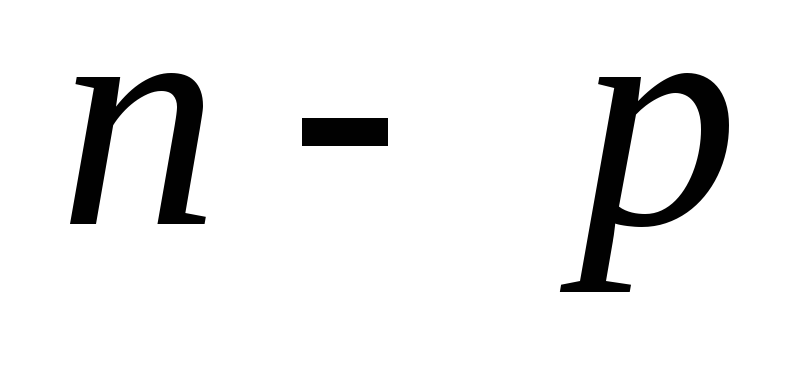 вершин связаны с этим циклом ребрами, т.к. граф связный. Следовательно,
вершин связаны с этим циклом ребрами, т.к. граф связный. Следовательно, 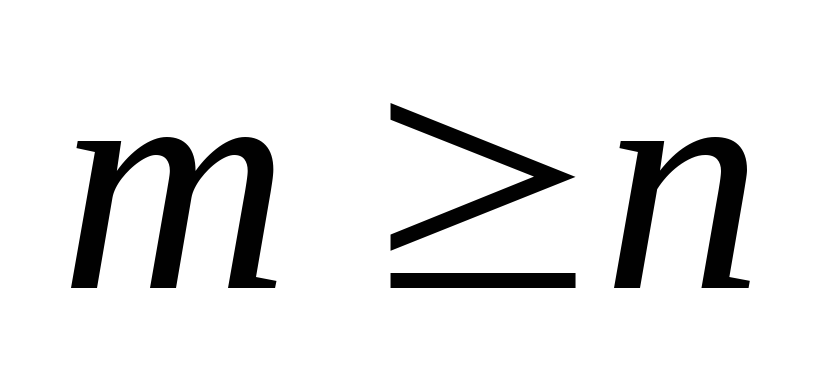 , что противоречит условию
, что противоречит условию 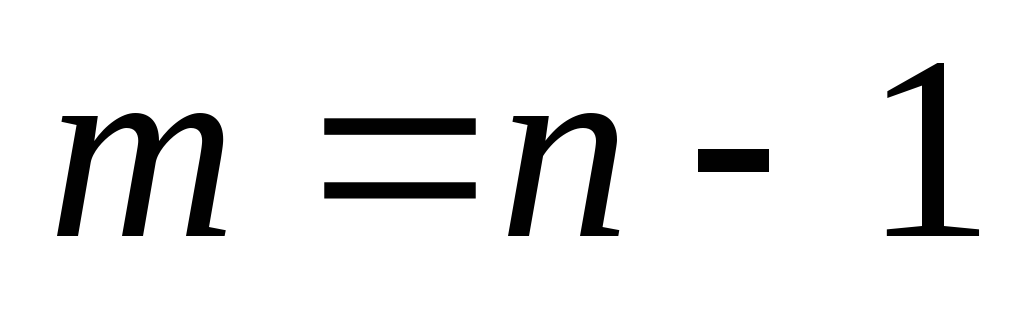 . Остальное без док-ва.
. Остальное без док-ва. 1. 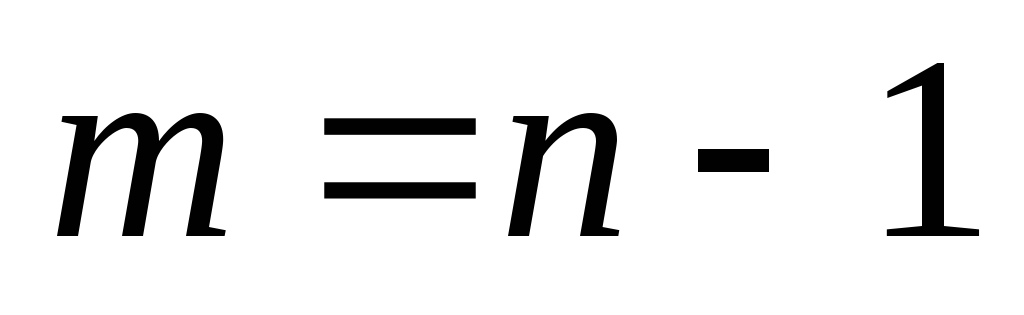
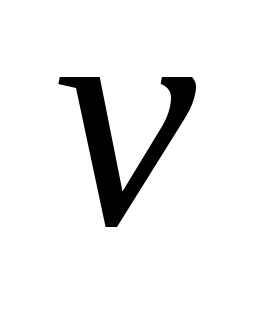
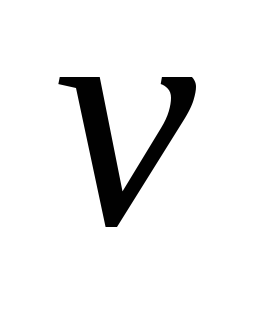
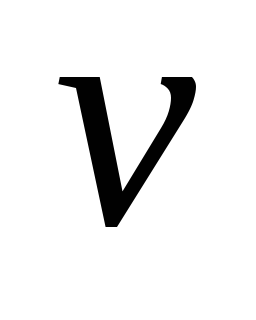
Источник

 — дерево.
— дерево. ациклический и
ациклический и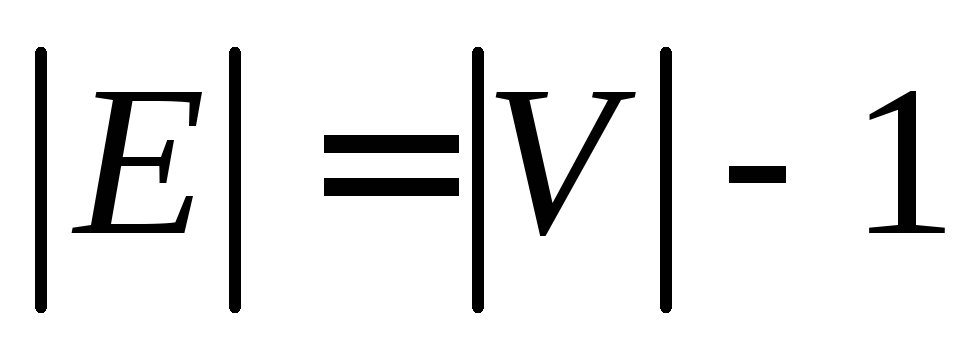 .
. связный и
связный и .
. связный и каждое его ребро является мостом.
связный и каждое его ребро является мостом. можно соединить, притом единственной, простой цепью.
можно соединить, притом единственной, простой цепью. ациклический, и добавление к нему нового ребра приводит к образованию единственного простого цикла.
ациклический, и добавление к нему нового ребра приводит к образованию единственного простого цикла.
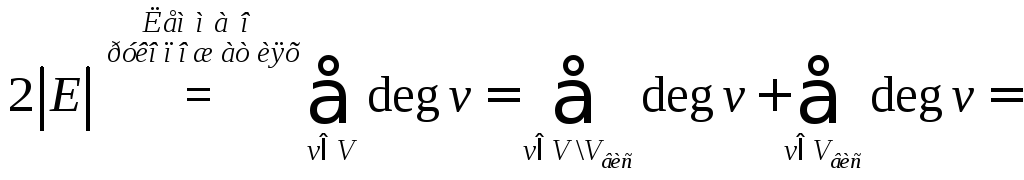

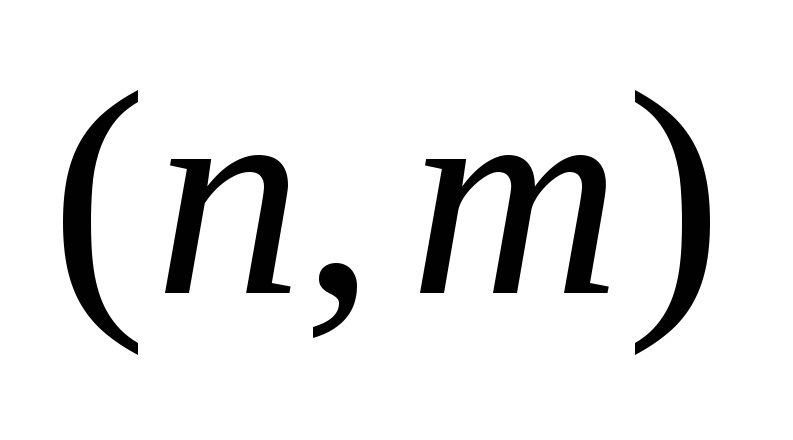 – графа
– графа  следующие утверждения эквивалентны:
следующие утверждения эквивалентны:  – дерево;
– дерево; соединяет единственная простая цепь;
соединяет единственная простая цепь; – связный граф, и любое ребро есть мост;
– связный граф, и любое ребро есть мост; – связный граф и древовидный;
– связный граф и древовидный; – ациклический граф (лес) и древовидный;
– ациклический граф (лес) и древовидный; – ациклический граф (лес) и субцикличекий;
– ациклический граф (лес) и субцикличекий; – связный, субциклический и неполный,
– связный, субциклический и неполный, 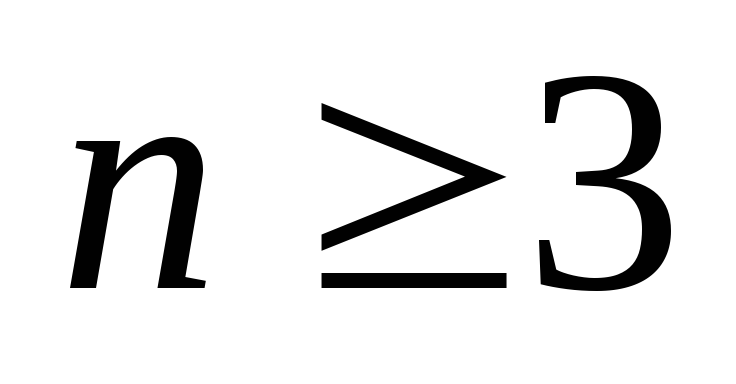 ;
; – древовидный и субциклический, исключая
– древовидный и субциклический, исключая 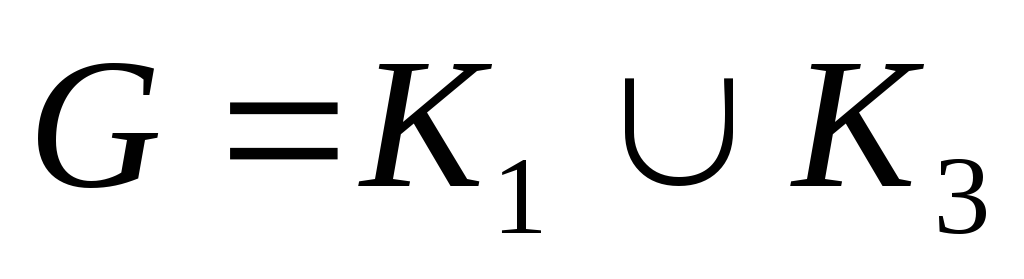 и
и 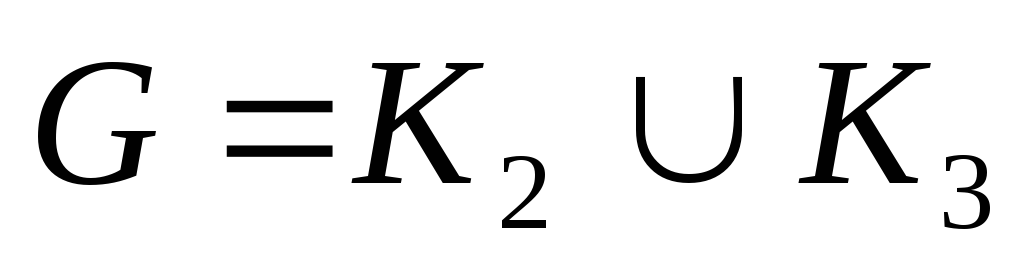 ;
;